A very long uniformly charge thred oriented along the axis of a circle of radius R=1m rests on its centre with one of the ends. The charge per unit length on the thread is . Find the flux of the vector E through the circle area in (Vm).
The correct Answer is:8
To find the electric flux through the area of a circle due to a uniformly charged thread, we can follow these steps:
1. Understand the Configuration:
- We have a long uniformly charged thread oriented along the axis of a circle with radius R=1m.
- The charge per unit length on the thread is given as λ=16ϵ0.
2. Identify the Electric Field:
- The electric field E due to an infinitely long charged thread at a distance y from the thread is given by the formula:
E=λ2πϵ0y
- Here, ϵ0 is the permittivity of free space.
3. Determine the Area Element:
- The area element dA for a thin ring of radius y and thickness dy is:
dA=2πydy
4. Calculate the Electric Flux:
- The electric flux Φ through the circle can be calculated using:
Φ=∫E⋅dA
- Since the electric field has a component along the radial direction (x-direction) and the area vector is perpendicular to the surface (y-direction), we only consider the x-component of E:
dΦ=E⋅dA=E⋅(2πydy)
5. Substituting for Electric Field:
- Substitute E into the flux equation:
dΦ=(λ2πϵ0y)(2πydy)=λϵ0dy
6. Integrate Over the Circle:
- Now we integrate from y=0 to y=R:
Φ=∫R0λϵ0dy=λϵ0∫R0dy=λϵ0(y)R0=λRϵ0
7. Substituting Known Values:
- Substitute λ=16ϵ0 and R=1m:
Φ=16ϵ0⋅1ϵ0=16Vm
8. Final Result:
- The electric flux through the circle area is:
Φ=8Vm
- We have a long uniformly charged thread oriented along the axis of a circle with radius R=1m.
- The charge per unit length on the thread is given as λ=16ϵ0.
- The electric field E due to an infinitely long charged thread at a distance y from the thread is given by the formula:
E=λ2πϵ0y
- Here, ϵ0 is the permittivity of free space.
- The area element dA for a thin ring of radius y and thickness dy is:
dA=2πydy
- The electric flux Φ through the circle can be calculated using:
Φ=∫E⋅dA
- Since the electric field has a component along the radial direction (x-direction) and the area vector is perpendicular to the surface (y-direction), we only consider the x-component of E:
dΦ=E⋅dA=E⋅(2πydy)
- Substitute E into the flux equation:
dΦ=(λ2πϵ0y)(2πydy)=λϵ0dy
- Now we integrate from y=0 to y=R:
Φ=∫R0λϵ0dy=λϵ0∫R0dy=λϵ0(y)R0=λRϵ0
- Substitute λ=16ϵ0 and R=1m:
Φ=16ϵ0⋅1ϵ0=16Vm
- The electric flux through the circle area is:
Φ=8Vm
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Part - IV
9 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 3 Part - I
33 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 2 Part - I
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
A very long uniformly charged wire oriented along the axis of a circular ring of radius R rests on its centre with one of the ends (as shown in figure). The linear charge density on the wire is λ. Evalute the flux of the vector →E across the circle area.

View SolutionA system consits fo a thin charged wire ring of radius R and a very long uniformly charged thread oriented along the axis of the ring, with one of its ends coinciding with the centre of the ring. The total charge of the ring, with one of the ring so equal to q. The charge of the thread (per unit length) is equal to λ. Find the interaction froce between the ring and the thread.
View SolutionA Charge Q is distributed uniformly on a ring of radius r. A sphere of equal r is constructed with its centre at the periphery of the ring (figure 30.12) Find the flux of the electric field through the surface of the sphere.
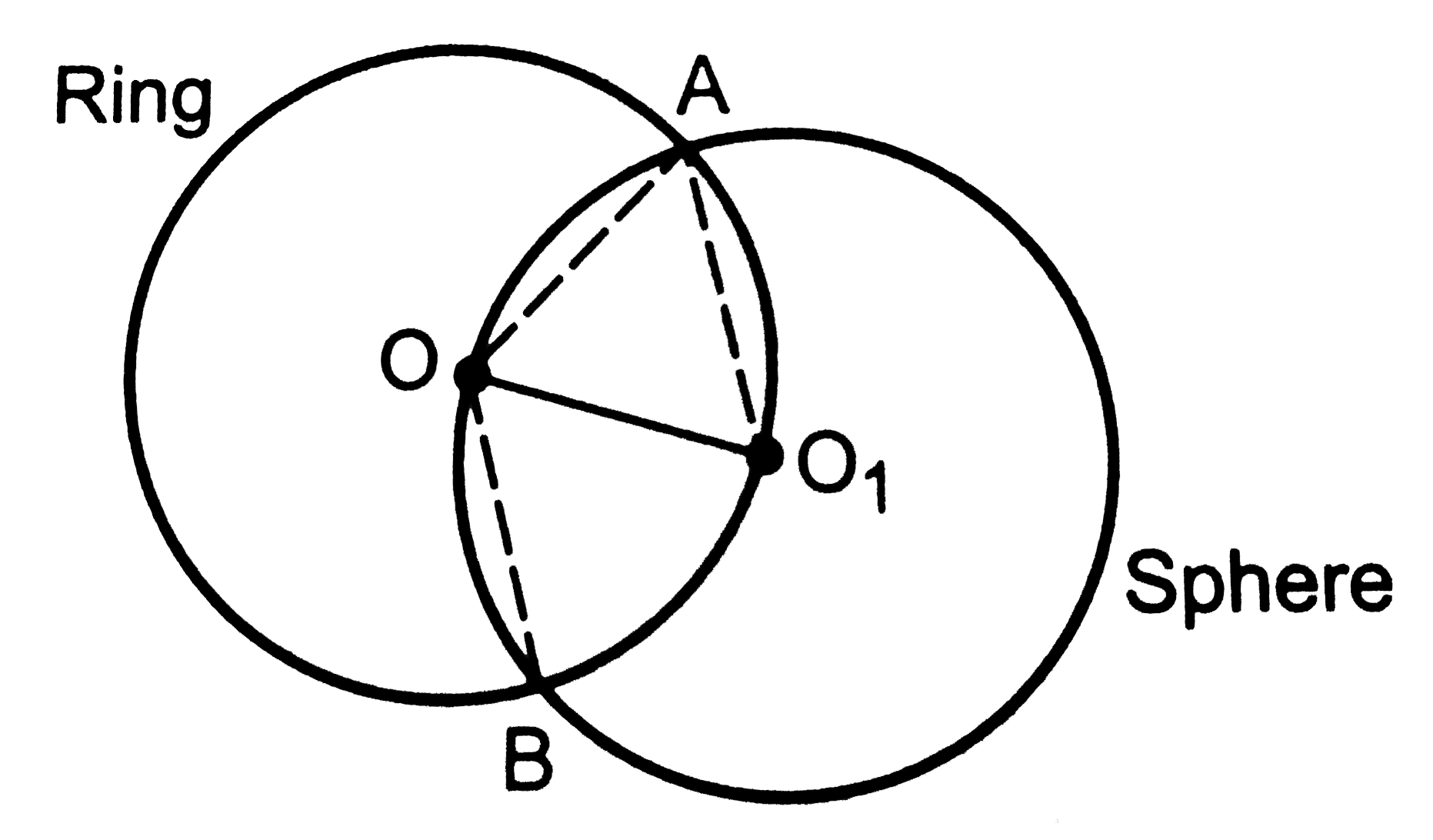
View Solution
A circular disc of radius b has a hole of radius a at its centre (see figure) if the mass per unit area of the disc varies as (σ0r) then the radius of gyration of the disc about its axis passing through the centre is
View SolutionA uniformly charged square plate having side L carries a uniform surface charge density σ. The plate lies in the y−z plane with its centre at the origin. A point charge q lies on the x-axis. The flux of the electric field of q through the plate is ϕ0, while the foce on the point charge q due to the plate is F0, along the x-axis. Then,
View SolutionA charge Q is uniformly distributed over a rod of length ι. Condider a hypothetical cube of edge ι with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformaly charged line charge( linear charge density λ) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
View SolutionA charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View SolutionA thin straight infinitely long conducting wire having charge density λ enclosed bya cylindrical surface of radius rand length lr, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionA thread carrying a unifrom charge λ per unit length has the configuration shown in fig, Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude fo the electric field strength at the point O.
 ,
, 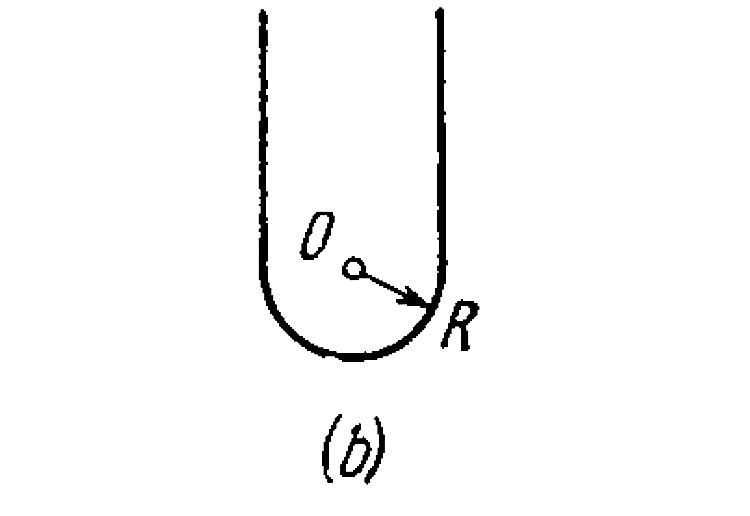
View Solution
