Two small balls of masses 3m and 2m and each having charges Q are connected by a string passing over a fixed pulley. Calculate the acceleration of the balls (in m/sec2) if the whole assembly is located in a uniform electric field E=mg2Q acting vertically downwards. Neglect any interaction between the balls. Take g=10m/s2
The correct Answer is:2
To solve the problem, we need to analyze the forces acting on each mass and apply Newton's second law of motion. Let's break it down step by step.
Step 1: Identify the forces acting on each mass
1. For the mass 3m:
- Weight acting downwards: W1=3mg
- Electric force acting downwards: Felectric=QE
- Tension in the string acting upwards: T
2. For the mass 2m:
- Weight acting downwards: W2=2mg
- Electric force acting downwards: Felectric=QE
- Tension in the string acting upwards: T
Step 2: Write the equations of motion for each mass
1. For mass 3m (moving downwards):
Fnet=W1+Felectric−T=3ma
Substituting the forces:
3mg+QE−T=3ma
2. For mass 2m (moving upwards):
Fnet=T−W2−Felectric=2ma
Substituting the forces:
T−2mg−QE=2ma
Step 3: Substitute the value of the electric field
Given that E=mg2Q, we can substitute this into our equations.
- For the electric force:
QE=Q(mg2Q)=mg2
Step 4: Rewrite the equations with the electric force substituted
1. For mass 3m:
3mg+mg2−T=3ma
Simplifying:
6mg2+mg2−T=3ma
7mg2−T=3ma(Equation 1)
2. For mass 2m:
T−2mg−mg2=2ma
Simplifying:
T−4mg2−mg2=2ma
T−5mg2=2ma(Equation 2)
Step 5: Solve the equations simultaneously
From Equation 1:
T=7mg2−3ma
Substituting T into Equation 2:
7mg2−3ma−5mg2=2ma
Simplifying:
2mg2−3ma=2ma
mg−3ma=2ma
mg=5ma
Dividing both sides by m:
g=5a
Thus, the acceleration a is:
a=g5
Substituting g=10m/s2:
a=105=2m/s2
Final Answer:
The acceleration of the balls is 2m/s2.
---
- Weight acting downwards: W1=3mg
- Electric force acting downwards: Felectric=QE
- Tension in the string acting upwards: T
- Weight acting downwards: W2=2mg
- Electric force acting downwards: Felectric=QE
- Tension in the string acting upwards: T
Fnet=W1+Felectric−T=3ma
Substituting the forces:
3mg+QE−T=3ma
Fnet=T−W2−Felectric=2ma
Substituting the forces:
T−2mg−QE=2ma
QE=Q(mg2Q)=mg2
3mg+mg2−T=3ma
Simplifying:
6mg2+mg2−T=3ma
7mg2−T=3ma(Equation 1)
T−2mg−mg2=2ma
Simplifying:
T−4mg2−mg2=2ma
T−5mg2=2ma(Equation 2)
T=7mg2−3ma
7mg2−3ma−5mg2=2ma
Simplifying:
2mg2−3ma=2ma
mg−3ma=2ma
mg=5ma
Dividing both sides by m:
g=5a
Thus, the acceleration a is:
a=g5
Substituting g=10m/s2:
a=105=2m/s2
The acceleration of the balls is 2m/s2.
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - IV
Explore 9 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise - 3 Part - I
Explore 33 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise - 2 Part - I
Explore 21 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
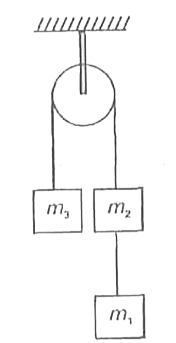
View SolutionThree blocks of masses m1=4kg,m2=2kg,m3=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m/s2)
View SolutionA ball is thrown vertically upwards. It returns 6 s later. Calculate the initial velocity of the ball. (Take g=10m s−2 )
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View SolutionTwo blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View SolutionThe weights W and 2W are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up with an acceleration of 10m/s2, the tension in the string will be (g=10m/s2)
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View Solution