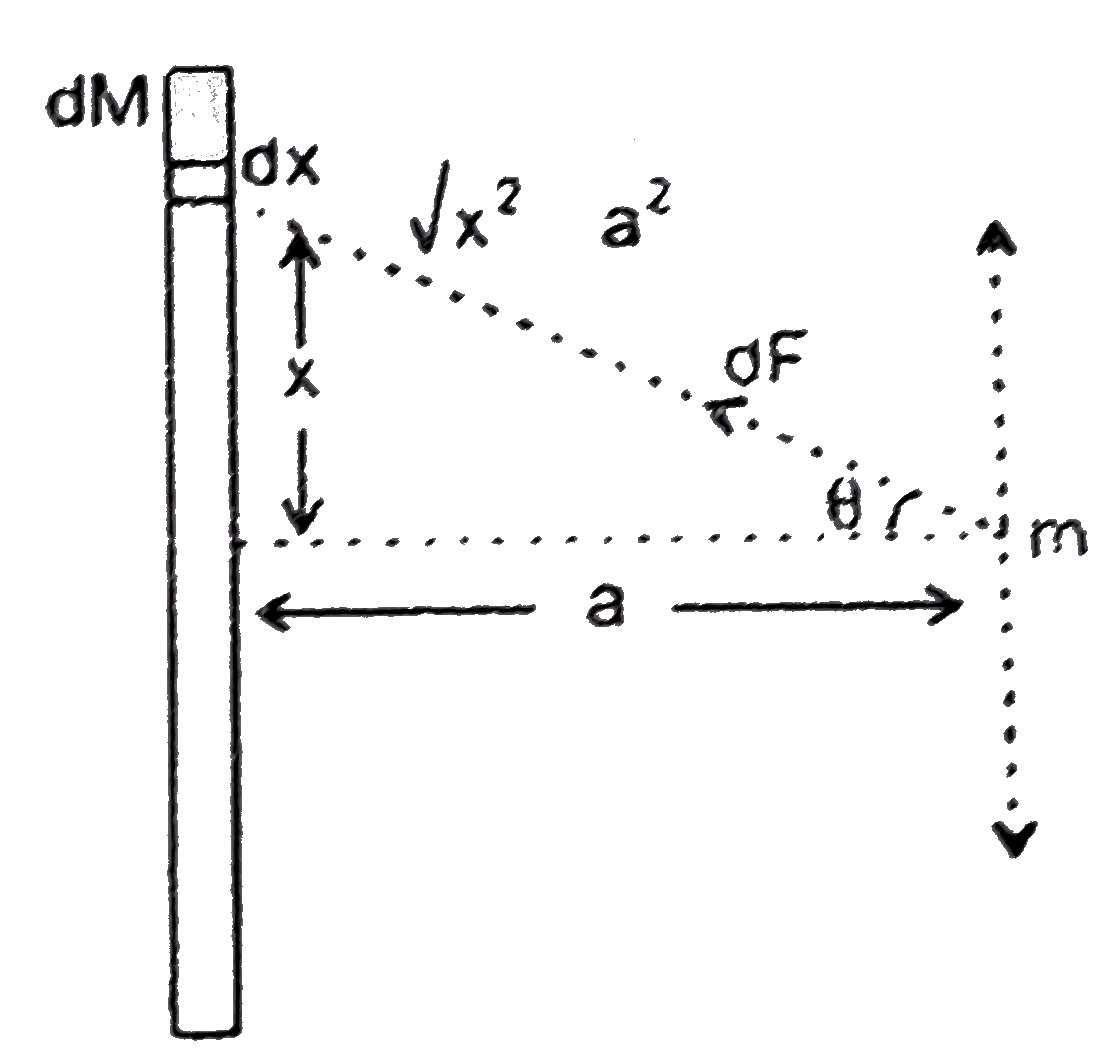
Calculate the force exerted by point mass m on rod of uniformly distributed mass M and length l (Placed as shown in figure)
 .
.
∵ Direction of force is changing at every element. We have to make components of force and then integrate.
Net vertical force =0
dF = force element =G.dM.m(x2+a2)
dFh=dFcosθ = Force on element in horizontal direction =G.dM.m(x2+a2)cosθ
∴Fh=∫G.M.mcosθdxl(x2+a2)=G.M.mll/2∫−l/2cosθ.dx(x2+a2)=GMmla2l/2∫−l/2cosθ.dxsec2θ
where x=a than θ then dx=asec2θdθ
=GMmla[sinθ]l/2l/2tanθ=xa,thesinθ=x√x2+a2
=GMmla[x√x2+a2]l/2−l/2=√GMmlla√l24+a2=GMma√(l24+a2)
 .
.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXAMPLE2videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-1 PART-19videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions16videos
NUCLEAR PHYSICS
Similar Questions
Calculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
 View Solution
View SolutionCharge Q is uniformly distributed on a dielectric rod AB of length 2l. The potential at P shown in the figure is equal to
 View Solution
View SolutionThe moment of inertia of a thing uniform rod of length L and mass M, about axis CD (as shown in figure) is
 View Solution
View SolutionFind aC and α of the smooth rod of mass m and length l.
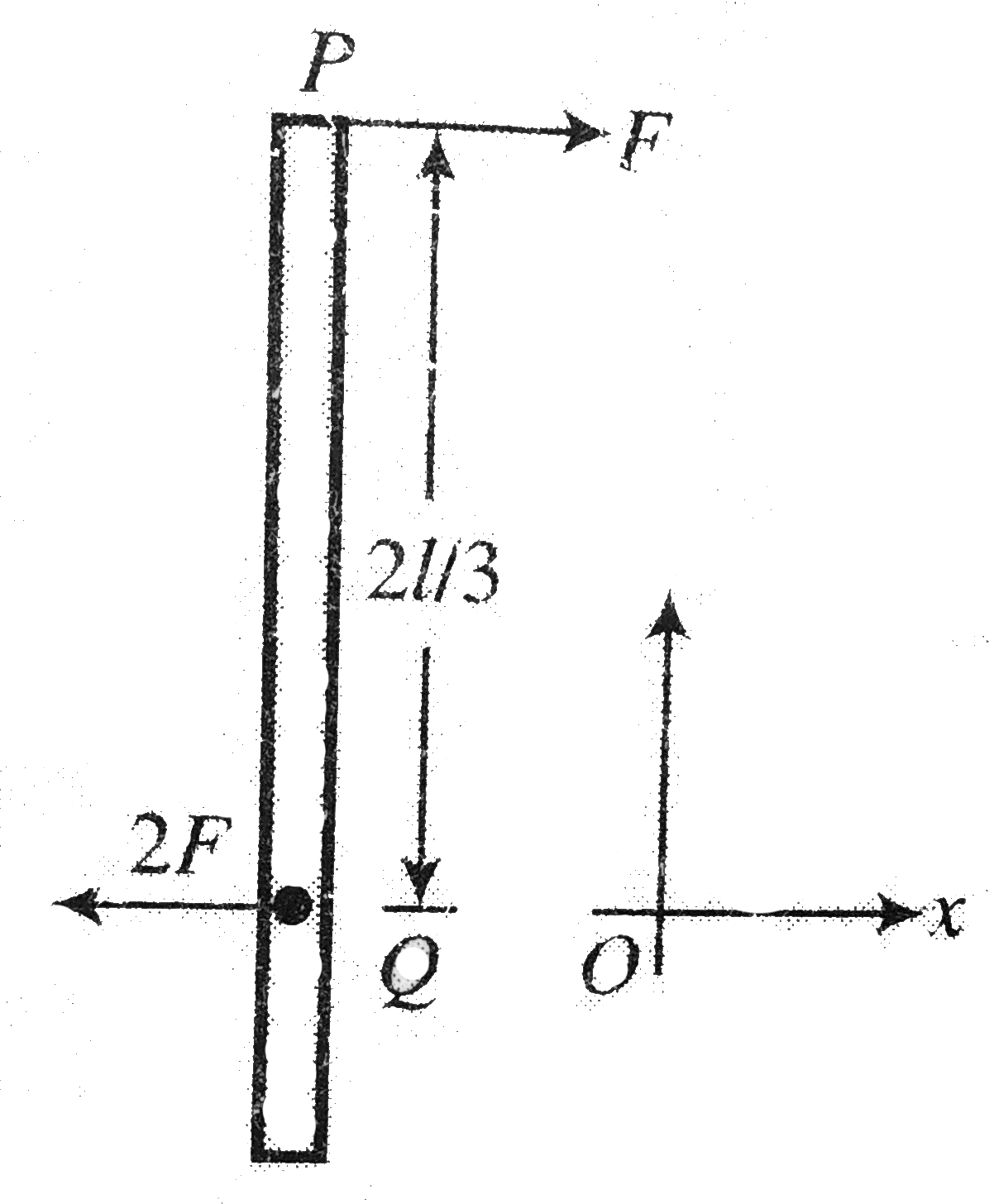 View Solution
View SolutionA straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is A+Bx2, is given by :
View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then:
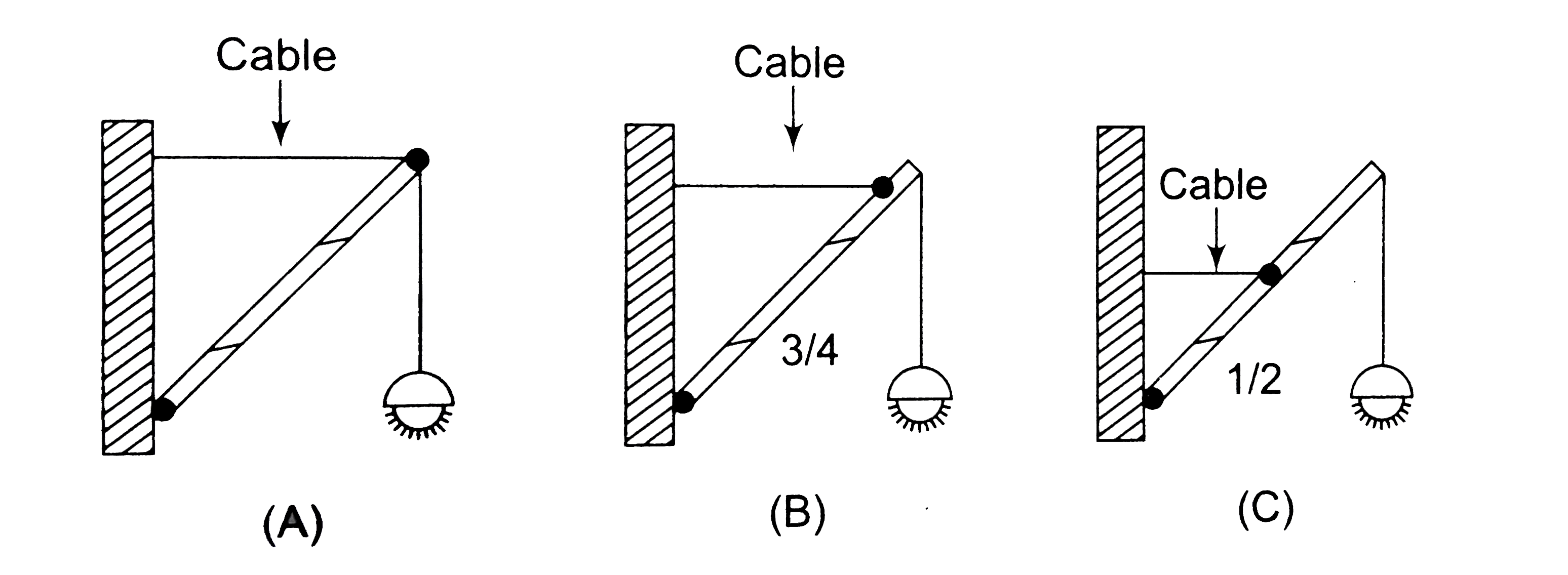 View Solution
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.
 View Solution
View SolutionA uniform rod of length l and mass m is hung from, strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?
 View Solution
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
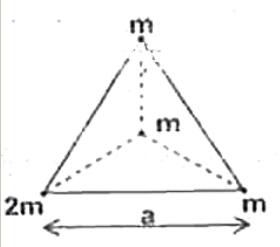
View SolutionThree point masses m,m and 2m are placed on the vertex of an equilateral triangle of side 'a' Another point mass 'm' is placed at the centroid of the triangle as shown in the figure. If the magnitude of net force on the point mass placed at centroid is KGm2a2 then find the value of K (G= universal gravitational constant )
 View Solution
View Solution

