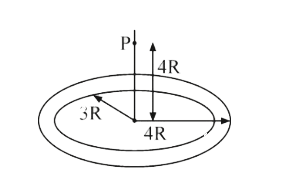
A thin uniform annular disc (see figure) of mass M has an outer radius 4R and an inner radius 3R. The work required to take a unit mass from point P on its axis to infinity is :

$\frac{2 G M}{7 R} (4 \sqrt{2} - 5)$

$- \frac{2 G M}{7 R} (4 \sqrt{2} - 5)$

$\frac{G M}{4 R}$

$\frac{2 G M}{5 R} (\sqrt{2} - 1)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video & image solution for A thin uniform annular disc (see figure) of mass M has an outer radius 4R and an inner radius 3R. The work required to take a unit mass from point P on its axis to infinity is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

A thin uniform annular disc (see figure) of mass M has an outer radius 4R and an inner radius 3R. The work required to take a unit mass from point P on its axis to infinity is :

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-GRAVITATION-EXERCISE-3 PART-1