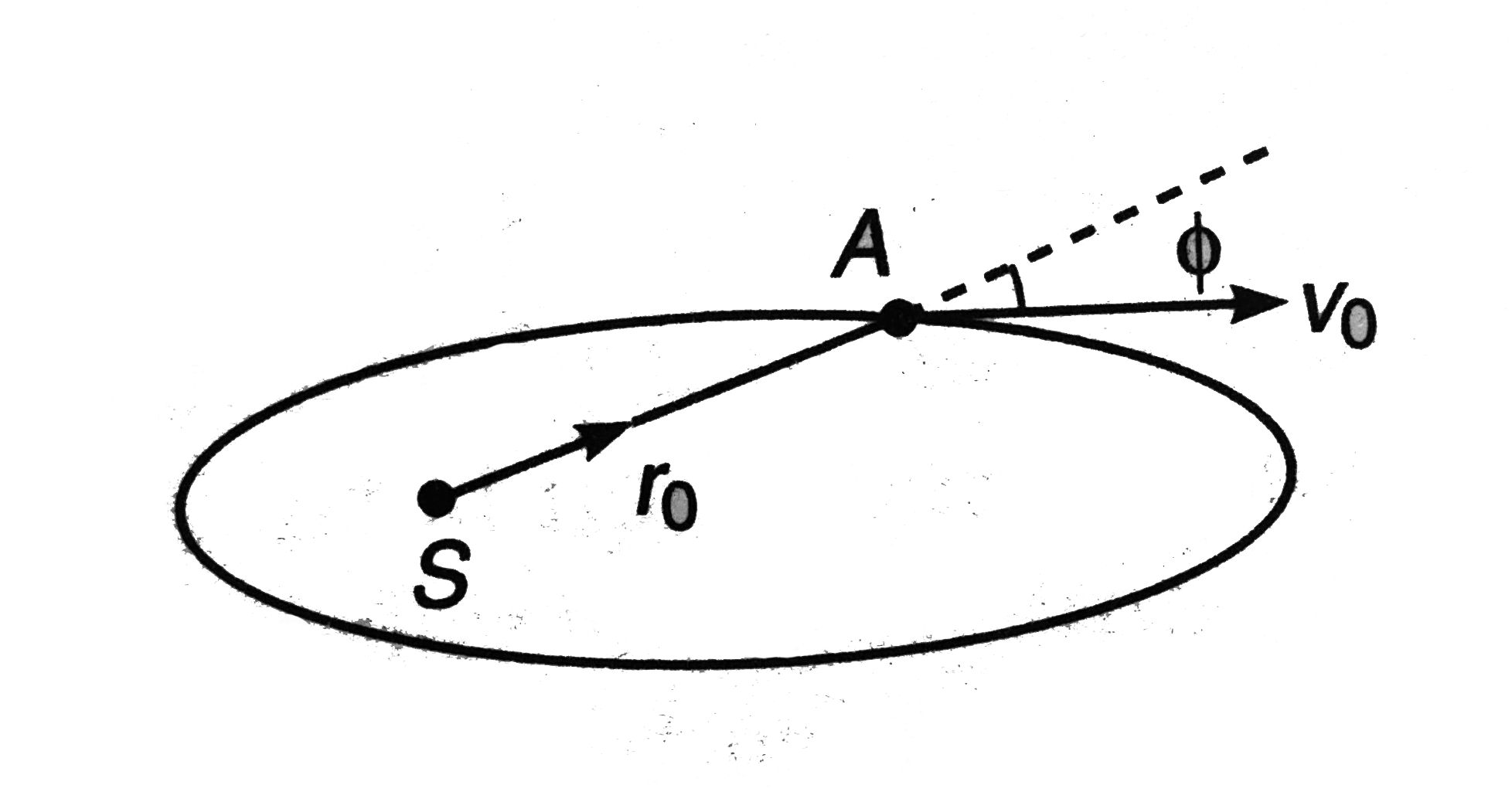
A planet A moves along an ellipticl orbit around the surface. At the moment when it was at the distance from the sun its velocity was equal to and the angle between radius vector and velocity vector was equal to . Find the maximum and minimum distance that will separate this planet from the sun during its orbital motion.
The correct Answer is:
where .
Step by step video & image solution for A planet A moves along an ellipticl orbit around the surface. At the moment when it was at the distance r_(0) from the sun its velocity was equal to v_(0) and the angle between radius vector r_(0) and velocity vector v_(0) was equal to alpha. Find the maximum and minimum distance that will separate this planet from the sun during its orbital motion. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-3 PART-2
11 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions
16 Videos
Similar Questions
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
View SolutionFind the maximum and minimum distances of the planet A from the sun S, if at a certain moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
View Solution
Knowledge Check
A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
Speed of a planet in an ellioptical orbit with semimajor axis a about sun of mass M at a distance r from sun is
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
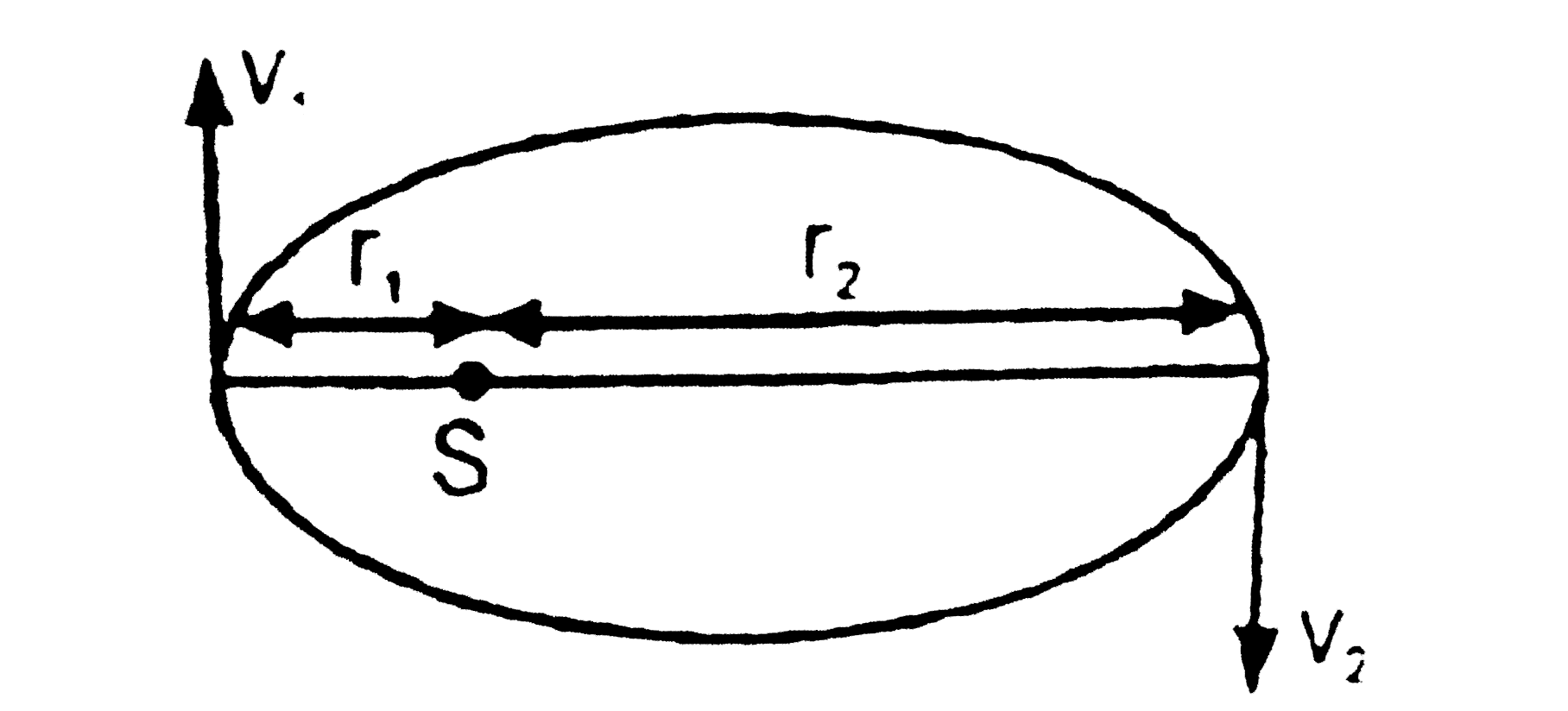
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
View SolutionA planet moves around the sun. It is closest to sun to sun at a distance d1 and have velocity v1 At farthest distance d2 its speed will be
View SolutionA planet of mass m moves along an ellipse around the Sun so that its maximum and minimum distances from the Sun are equal to r1 and r2 respectively. Find the angular momentum M of this planet relative to the centre of the Sun.
View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance r1 and farthest away at a distance of r2. If v1 and v2 are the linear velocities at these points respectively, then the ratio v1v2 is
View Solution
