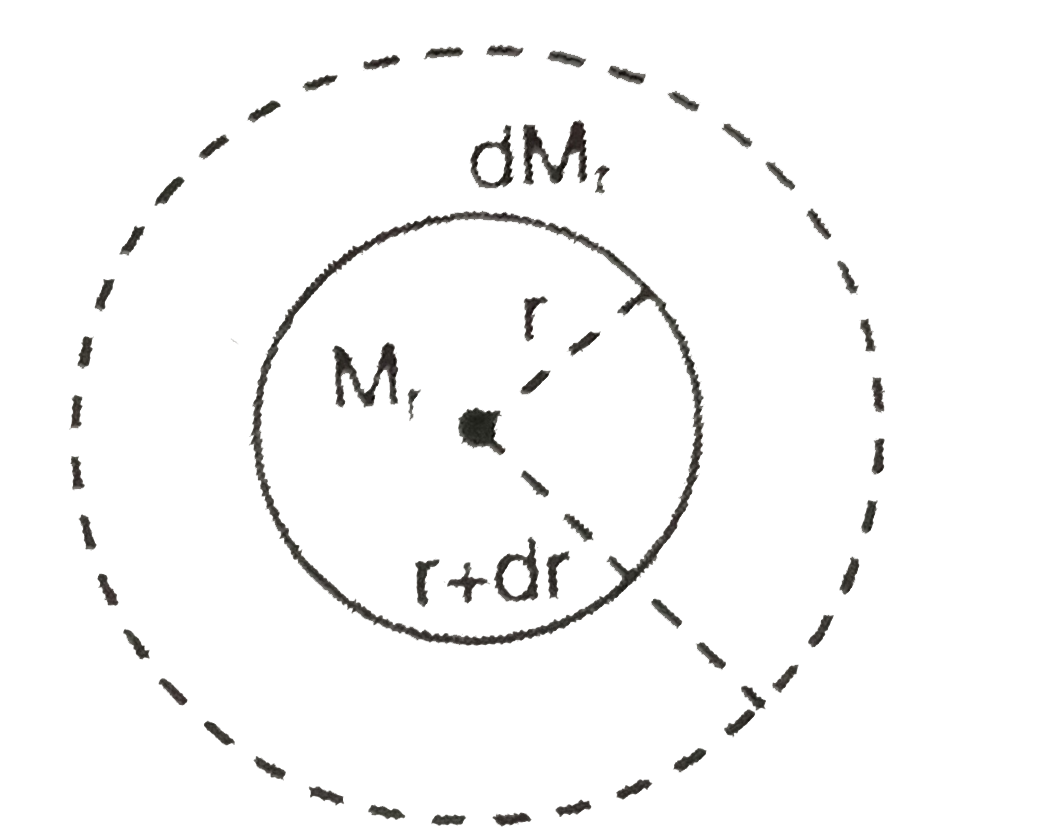
A star can be considered as a shpherical ball of hot gas of radius R.Inside the star the density of the gas is $ρ_{r}$ at a radius r and mass of the gas within this region is $M_{r}$ .The correct differential equation for variation of mass with respect to radius $(\frac{d M_{r}}{d t})$ is (refer to the adjacent figure)

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $2.10 \times 10^{7}$

Updated on:21/07/2023

Answer

Step by step video & image solution for A star can be considered as a shpherical ball of hot gas of radius R.Inside the star the density of the gas is rho_r at a radius r and mass of the gas within this region is M_r.The correct differential equation for variation of mass with respect to radius ((dM_r)/(dt)) is (refer to the adjacent figure) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

The moment of inertia of a hoop of radius R and mass M, about any tangent
A $[3 m R^{2}] / 2$
B $[m R^{2}] / 2$
C $M R^{2}$
D $[M R^{2}] / 4$
A point mass m is placed inside a spherical shell of radius R and mass M at a distance $\frac{R}{2}$ form the centre of the shell. The gravitational force exerted by the shell on the point mass is
A $\frac{G M m}{R^{2}}$
B $\frac{2 G M m}{R^{2}}$
Czero
D $\frac{4 M m}{R^{2}}$