The base BC of a triangle ABC is bisected at the point (p,q) and the equations to the sides AB and AC are px+qy=1 and qx+py=1. The equation of the median through A is
(p−2q)x+(q−2p)y+1=0
(p+q)(x+y)−2=0
(2pq−1)(px+qy−1)=(p2+q2−1)(qx+py−1)
None of these
The correct Answer is:A
Step by step video solution for The base BC of a triangle ABC is bisected at the point (p,q) and the equations to the sides AB and AC are px +qy = 1 and qx +py = 1. The equation of the median through A is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The base BC of a triangle ABC is bisected at the point (a, b) and equation to the sides AB and AC are respectively ax+by=1 and bx+ay=1 Equation of the median through A is:
View SolutionThe base BC of a ABC is bisected at the point (p,q) & the equation to the side AB&AC are px+qy=1 & qx+py=1 . The equation of the median through A is: (p−2q)x+(q−2p)y+1=0 (p+q)(x+y)−2=0 (2pq−1)(px+qy−1)=(p2+q2−1)(qx+py−1) none of these
View SolutionD is the mid-point of side BC of a triangle ABC.AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE:EX=3:1.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
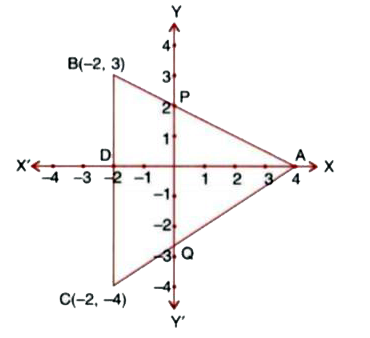
Find the equation of the line AC.
View SolutionIn an isosceles triangle ABC, the coordinates of the points Band C on the base BC are respectively (1,2) and (2.1). If the equation of the line AB is y=2x, then the equation of the line AC is
View SolutionThe equation of the sides of a triangle are x+2y+1=0,2x+y+2=0andpx+qy+1=0 and area of triangle is Δ .
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
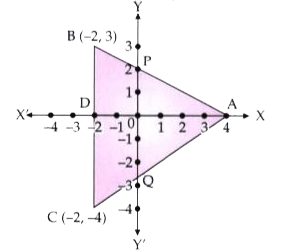
(iv) Find the equation of the line AC.
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If AC = 1, then the length of the median of triangle ABC through the vertex A is equal to
View SolutionLet ΔABC is an isosceles trianlge with AB=AC. If B=(0,a),C=(2a,0) and the equation of AB is 3x−4y+4a=0, then the equation of side AC is
View Solution
