Consider a chessboard of size 8 units ×8 units (i.e., each small square on the board has a side length of 1 unit). Let S be the set of all the 81 vertices of all the squares on the board. What is number of line segments whose vertices are in S1 and whose length is a positive integer? (The segments need not be parallel to the sides of the board).
The correct Answer is:780
To find the number of line segments whose vertices are in the set S (the set of all 81 vertices of the squares on an 8x8 chessboard) and whose length is a positive integer, we can break the problem down into several steps.
1. Understanding the Chessboard:
The chessboard has dimensions of 8 units by 8 units, which means it has 9 vertices along each side (0 to 8). Thus, the total number of vertices |S| is 9×9=81.
2. Identifying Line Segments:
We need to count the line segments formed by pairs of vertices in S that have integer lengths. The length of a line segment between two vertices (x1,y1) and (x2,y2) can be calculated using the distance formula:
d=√(x2−x1)2+(y2−y1)2
For d to be a positive integer, (x2−x1)2+(y2−y1)2 must be a perfect square.
3. Calculating Possible Lengths:
The maximum distance between any two vertices on the chessboard occurs between the corners, which is:
dmax=√(8−0)2+(8−0)2=√64+64=√128=8√2
However, we are only interested in integer lengths. The possible integer lengths can be from 1 to 8 (the maximum horizontal or vertical distance).
4. Counting Segments for Each Integer Length:
We will count the number of line segments for each integer length n from 1 to 8.
- Length 1:
- Segments parallel to axes: 8×9×2=144 (8 horizontal and 8 vertical segments).
- Diagonal segments: 8×8=64 (each square contributes 1 diagonal).
- Total for length 1: 144+64=208.
- Length 2:
- Segments parallel to axes: 7×9×2=126.
- Diagonal segments: 7×7=49.
- Total for length 2: 126+49=175.
- Length 3:
- Segments parallel to axes: 6×9×2=108.
- Diagonal segments: 6×6=36.
- Total for length 3: 108+36=144.
- Length 4:
- Segments parallel to axes: 5×9×2=90.
- Diagonal segments: 5×5=25.
- Total for length 4: 90+25=115.
- Length 5:
- Segments parallel to axes: 4×9×2=72.
- Diagonal segments: 4×4=16.
- Total for length 5: 72+16=88.
- Length 6:
- Segments parallel to axes: 3×9×2=54.
- Diagonal segments: 3×3=9.
- Total for length 6: 54+9=63.
- Length 7:
- Segments parallel to axes: 2×9×2=36.
- Diagonal segments: 2×2=4.
- Total for length 7: 36+4=40.
- Length 8:
- Segments parallel to axes: 1×9×2=18.
- Diagonal segments: 1×1=1.
- Total for length 8: 18+1=19.
5. Summing All Lengths:
Now, we sum the total segments for each length:
208+175+144+115+88+63+40+19=1080
Final Answer:
The total number of line segments whose vertices are in S and whose length is a positive integer is 1080.
The chessboard has dimensions of 8 units by 8 units, which means it has 9 vertices along each side (0 to 8). Thus, the total number of vertices |S| is 9×9=81.
We need to count the line segments formed by pairs of vertices in S that have integer lengths. The length of a line segment between two vertices (x1,y1) and (x2,y2) can be calculated using the distance formula:
d=√(x2−x1)2+(y2−y1)2
For d to be a positive integer, (x2−x1)2+(y2−y1)2 must be a perfect square.
The maximum distance between any two vertices on the chessboard occurs between the corners, which is:
dmax=√(8−0)2+(8−0)2=√64+64=√128=8√2
However, we are only interested in integer lengths. The possible integer lengths can be from 1 to 8 (the maximum horizontal or vertical distance).
We will count the number of line segments for each integer length n from 1 to 8.
- Segments parallel to axes: 8×9×2=144 (8 horizontal and 8 vertical segments).
- Diagonal segments: 8×8=64 (each square contributes 1 diagonal).
- Total for length 1: 144+64=208.
- Segments parallel to axes: 7×9×2=126.
- Diagonal segments: 7×7=49.
- Total for length 2: 126+49=175.
- Segments parallel to axes: 6×9×2=108.
- Diagonal segments: 6×6=36.
- Total for length 3: 108+36=144.
- Segments parallel to axes: 5×9×2=90.
- Diagonal segments: 5×5=25.
- Total for length 4: 90+25=115.
- Segments parallel to axes: 4×9×2=72.
- Diagonal segments: 4×4=16.
- Total for length 5: 72+16=88.
- Segments parallel to axes: 3×9×2=54.
- Diagonal segments: 3×3=9.
- Total for length 6: 54+9=63.
- Segments parallel to axes: 2×9×2=36.
- Diagonal segments: 2×2=4.
- Total for length 7: 36+4=40.
- Segments parallel to axes: 1×9×2=18.
- Diagonal segments: 1×1=1.
- Total for length 8: 18+1=19.
Now, we sum the total segments for each length:
208+175+144+115+88+63+40+19=1080
The total number of line segments whose vertices are in S and whose length is a positive integer is 1080.
Topper's Solved these Questions
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-I: Previous Asked Question for Pre RMO)
17 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - High Level Problems (HLP)
35 Videos
- DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCE ENGLISHCHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - High Level Problem
26 Videos
Similar Questions
Consider square ABCD of side length 1. Let P be the set of all segments of length 1 with endpoints on the adjacent sides of square ABCD . The midpoints of segments in P enclose a region with area A. The value of A is (a) π4 (b) 1−π4 (c) 4−π4 (d) none of these
View SolutionThe following figures are made of 5 squares each square has side of 1 unit length. Find the perimeter of each of the given
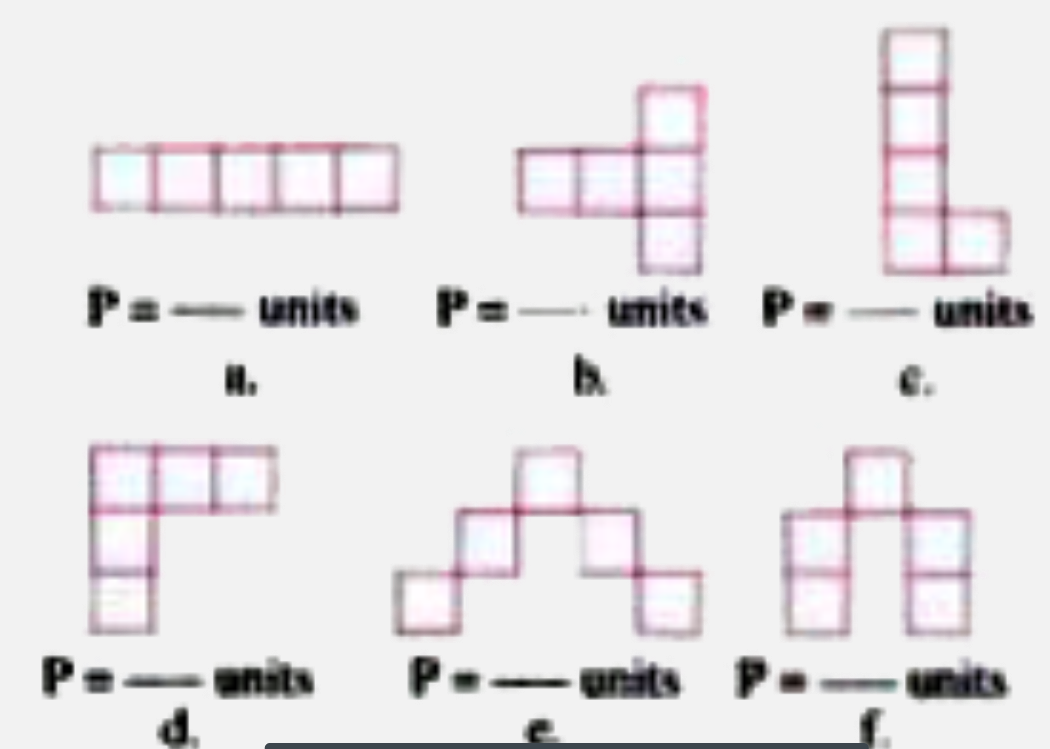
View Solution
Knowledge Check
In the grid shown below , each small square has a side length of 1 unit . In the shaded region , each vertex lies on a vertex of a small square . What is the area , in square units , of the shaded region ?
 A35B25C24D19
A35B25C24D19A square field measures 10 meters by 10 meters. Ten students each mark off a randomly selected region of the field, each region is square and has side lengths of 1 meter, and no two regions overlap. The students count the earthworms contained in the soil to a depth of 5 centimeters beneath the ground’s surface in each region. The results are shown in the table below.
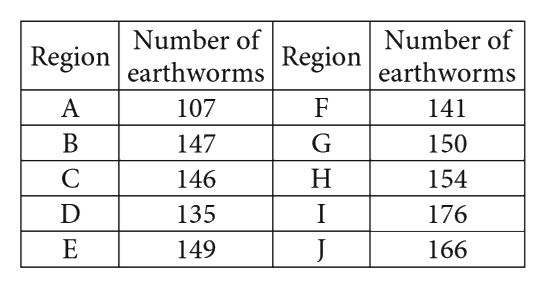
Which of the following is a reasonable approximation of the number of earthworms to a depth of 5 centimeters beneath the ground’s surface in the entire field?A150B1500C15000D150000
In the Figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionABCD is a square of side length 2 units. C1 is the circle touching all the sides of the square ABCD and C2 is the circumcircle of square ABCD. L is a fixed line in the same plane and R is fixed point. If a circle is such that it touches the line L and the circle C1 externally, such that both the circles are on the same side of the line, then the locus of centre of the circle is
View SolutionEach side of a square has length 4 units and its center is at (3,4). If one of the diagonals is parallel to the line y=x, then anser the following questions.
The radius of the circle inscribed in the triangle formed by any three vertices is
View SolutionLet S1,S2,S3, …. Are squares such that for each n≥1, The length of the side of Sn is equal to length of diagonal of Sn+1. If the length of the side S1 is 10 cm then for what value of n, the area of Sn is less than 1 sq.cm.
View SolutionLet S be the set of all triangles in the xy-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in S has area 50 eq. units, then the number of elements in the set S is
View Solution
