Gaussian surface does not include any net charge. Does it mean E=O ?
No, there can be electic field on the sufface of Gaussian suface but parallel to the surface.
Similar Questions
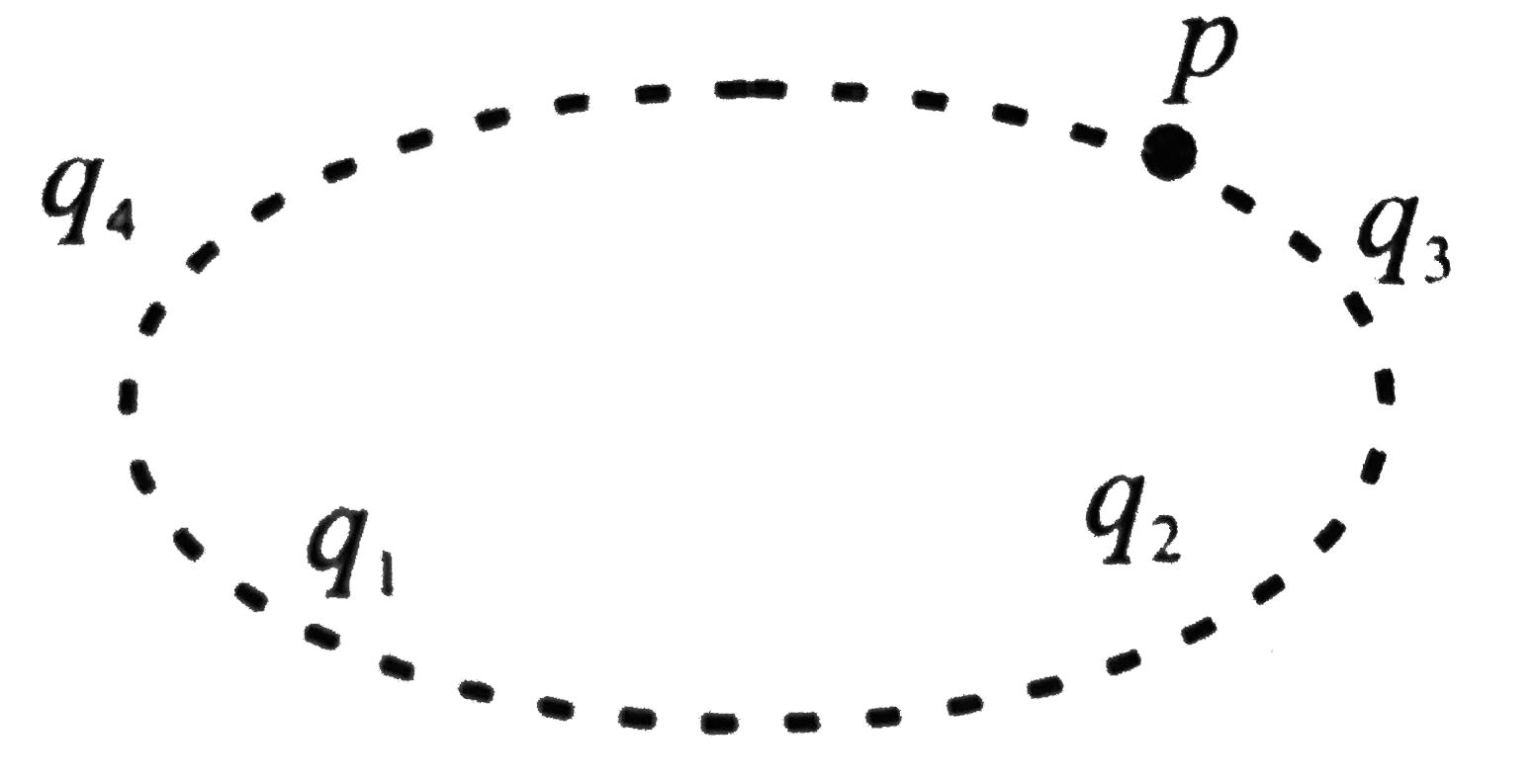
Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
View Solution
Knowledge Check
e- commerce does not include
A(a) A business's interactions with its suppliersB(b) A business's interactions with its customersC(c) Interactions among the various department within the business.D(d) Interactions among the geographically dispersed unit of the business.e-commerce does not include
AA business's interactions with its suppliersBA business's interactions with its customers.CInteractions among the various departments within the businessDInteractions among the geographically dispersed units of the businessAssertion(A):If Gaussian surface does not enclose any charge then →E at any point on the Gaussian surface must be zero.
Assertion(R ):No net charge is enclosed by Gaussians surface,so net flux passing through the surface is zero.ABoth A and R are true and R is the correct explanation of ABBoth A and R are True but R is not the correct explanation of A.CA is true and R is falseDA is false and R is true.
Choose the incorrect statement :
(a) The electric lines of force entering into A Gaussian surface provide nagative flux.
(b) A charge 'q' is placed at the centre of a cube .The flux through all the faces will be the same .
(c ) In uniform electric field net through a closed Gaussian surface containing no net charge ,is zero .
(d) When electric field is parallel to a Gaussian surface ,it provides a finite non -zero flux. Choose the most appropriate answer from the options given below :
View SolutionGaussian surface should not pass through any discrete charge because:
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are

View SolutionStatement-1: Suppose that a Gaussian surface enclose no net charge. Gauss law requires that electric field equals zero for all points on the surface.
Statement-2: If electric field equals zero everywhere on the surface, Gauss law requires that there be no net charge inside.
View Solution
