If net flux through a Gaussian surface is zero, then find whether the following statements are correct or not.
The net charge inside the surface is zero.
To determine whether the statement "The net charge inside the surface is zero" is correct when the net flux through a Gaussian surface is zero, we can use Gauss's Law. Here’s the step-by-step solution:
Step 1: Understand Gauss's Law
Gauss's Law states that the electric flux (Φ) through a closed surface (Gaussian surface) is directly proportional to the net charge (Q_enc) enclosed within that surface. Mathematically, it is expressed as:
Φ=Qencϵ0
where:
- Φ is the electric flux through the surface,
- Qenc is the net charge enclosed by the surface,
- ϵ0 is the permittivity of free space.
Step 2: Analyze the Given Condition
The problem states that the net flux through the Gaussian surface is zero:
Φ=0
Step 3: Apply Gauss's Law
Substituting the zero flux into Gauss's Law gives:
0=Qencϵ0
Step 4: Solve for the Enclosed Charge
From the equation above, we can deduce:
Qenc=0×ϵ0=0
This indicates that the net charge enclosed within the Gaussian surface is zero.
Step 5: Conclusion
Since we have determined that the net charge inside the Gaussian surface is indeed zero when the net flux is zero, we can conclude that the statement "The net charge inside the surface is zero" is correct.
Final Answer
The statement is true.
---
Gauss's Law states that the electric flux (Φ) through a closed surface (Gaussian surface) is directly proportional to the net charge (Q_enc) enclosed within that surface. Mathematically, it is expressed as:
Φ=Qencϵ0
where:
- Φ is the electric flux through the surface,
- Qenc is the net charge enclosed by the surface,
- ϵ0 is the permittivity of free space.
The problem states that the net flux through the Gaussian surface is zero:
Φ=0
Substituting the zero flux into Gauss's Law gives:
0=Qencϵ0
From the equation above, we can deduce:
Qenc=0×ϵ0=0
This indicates that the net charge enclosed within the Gaussian surface is zero.
Since we have determined that the net charge inside the Gaussian surface is indeed zero when the net flux is zero, we can conclude that the statement "The net charge inside the surface is zero" is correct.
The statement is true.
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) FILL IN THE BLANKS
4 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - II & III
15 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - EXERCISE
10 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
If net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
There are no changes inside the surface.
View SolutionIf net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
The number of field lines entering the surface equals to the number of field lines leaving the surface.
View Solution
Knowledge Check
If the net electric flux through a closed surface is zero, then we can infer
Ano net charge is enclosed by the surfaceBuniform electric field exists within the surfaceCelectric potential varies from point to point inside the surfaceDcharge is present inside the surfaceThe electric flux through a closed Gaussian surface depends upon
Anet charge enclosed and permittivity of the medium.Bnet charge enclosed, permittivity of the medium and the size of the Gaussian surface.Cet charge enclosed only.Dpermittivity of the medium only.If the size of the gaussian surface increases, the flux through the body:
AdecreasesBIncreasesCremains the sameDfluctuates
Find out flux through given gaussian surface.
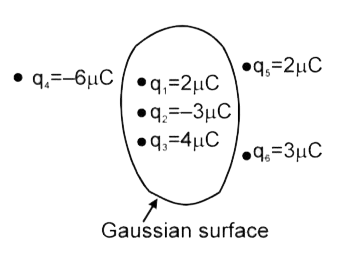
View SolutionIf electric flux passing through a close surface is zero then :-
View SolutionFind out flux through the given Gaussian surface.

View SolutionIn which of the following cases the net force is zero .
View SolutionIn which of the following cases the net force is zero?
View Solution
