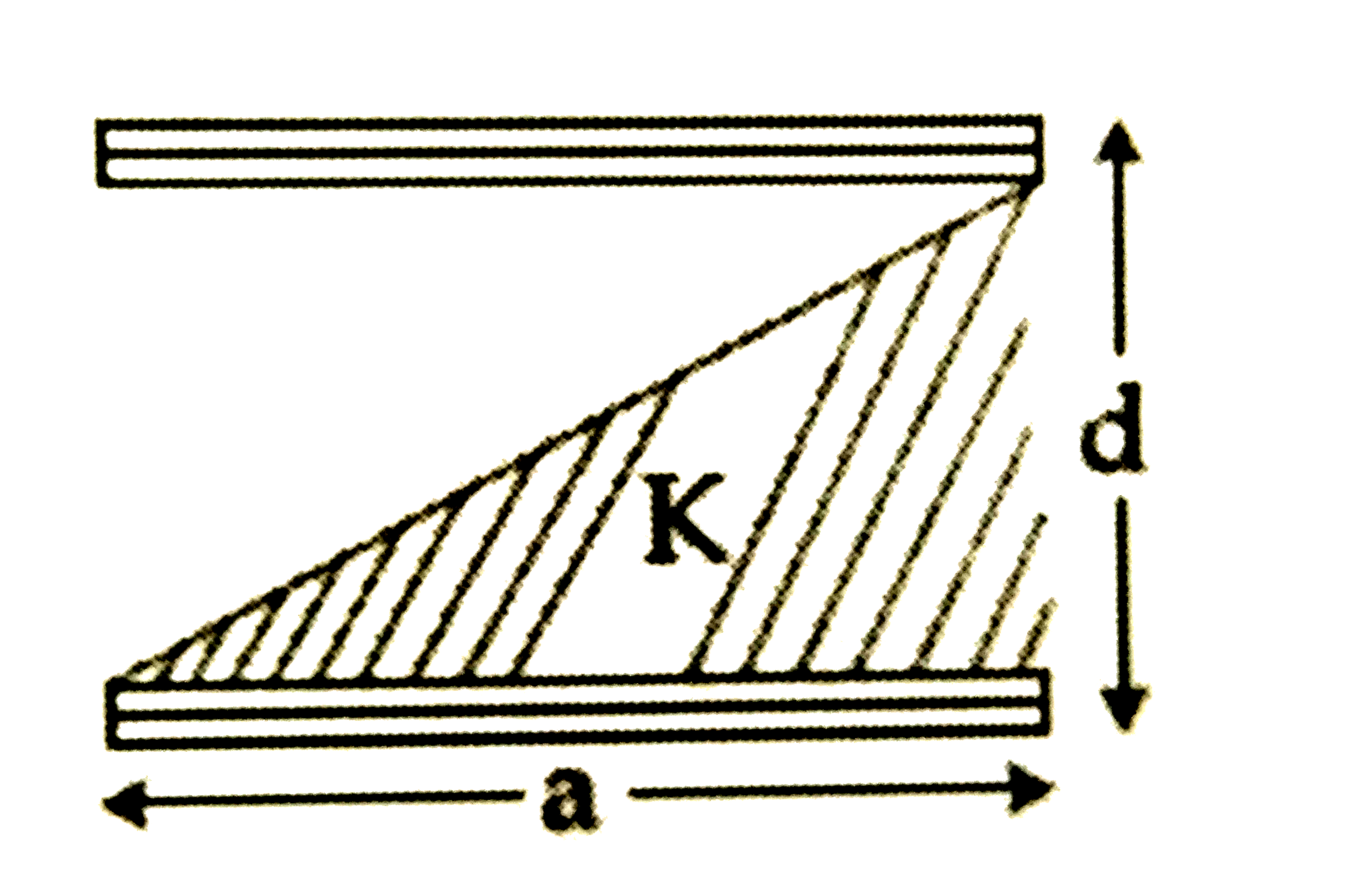
A parallel plate capacitor is made of two square plates of side 'a' , separated by a distance d much less than a. The lower triangular portion is filled with a dielectric of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
 a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
12Kε0a2d
ε0a2dInK
Kε0a2d(K−1)InK
Kε0a22d(K+1)
The correct Answer is:C
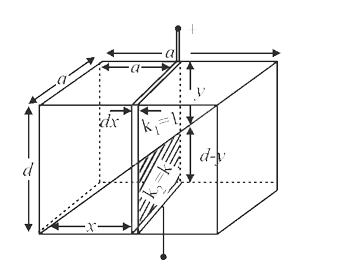
For vacuum k1=1
For dielectric k2=k
Consier two elemental slabs. (one in vacum and other in dielectric) having capacitances dC1 and dC2.dC1 and dC2 are in series.
1dC=1dC1+1dC2=yε0k1adx+d−yε0k2adx,dC= Capitances of composite elemental slabs.
⇒1dC=k2y+(d−y)k1ε0k1k2adx=ky+d−yε0kadx
All such dC's are in parallel.
∴ Total capacitance C=∫dC=ε0ka∫dxky+d−y....i
Now d−yx=da⇒x=(d−y)ad.......ii
From equation i and ii
C=ε0ka[ad]∫d0dy(k−1)y+d=ε0ka2dIn[(k−1)y+d]d0(k−1)
C=ε0ka2dInk(k−1)
Topper's Solved these Questions
Similar Questions
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 View Solution
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 View Solution
View SolutionA capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constants K1andK2 are filled in the gap as shown in fig. Find the capacitance.
 View Solution
View SolutionAir filled capacitor of capacitance 2μF is filled with three dielectric material of dielectric constant K1=4,K2=4 and K3=6 as shown in the figure . The new capacitance of the capacitor is
View SolutionA parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(x)=K(1+ax) where ‘x’ is shown in figure. If (al)<<1 , the total capacitance of the system is best given by the expression:
 View Solution
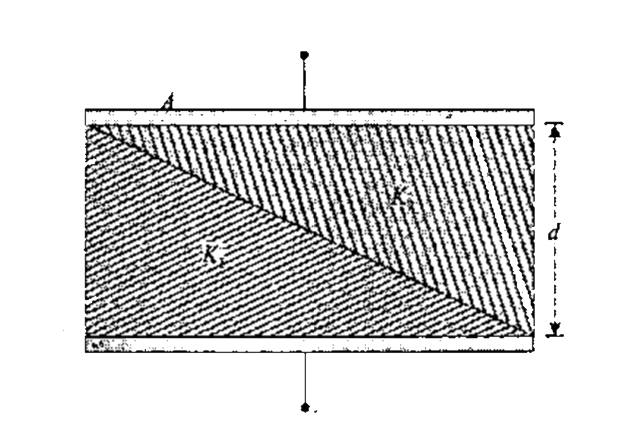
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
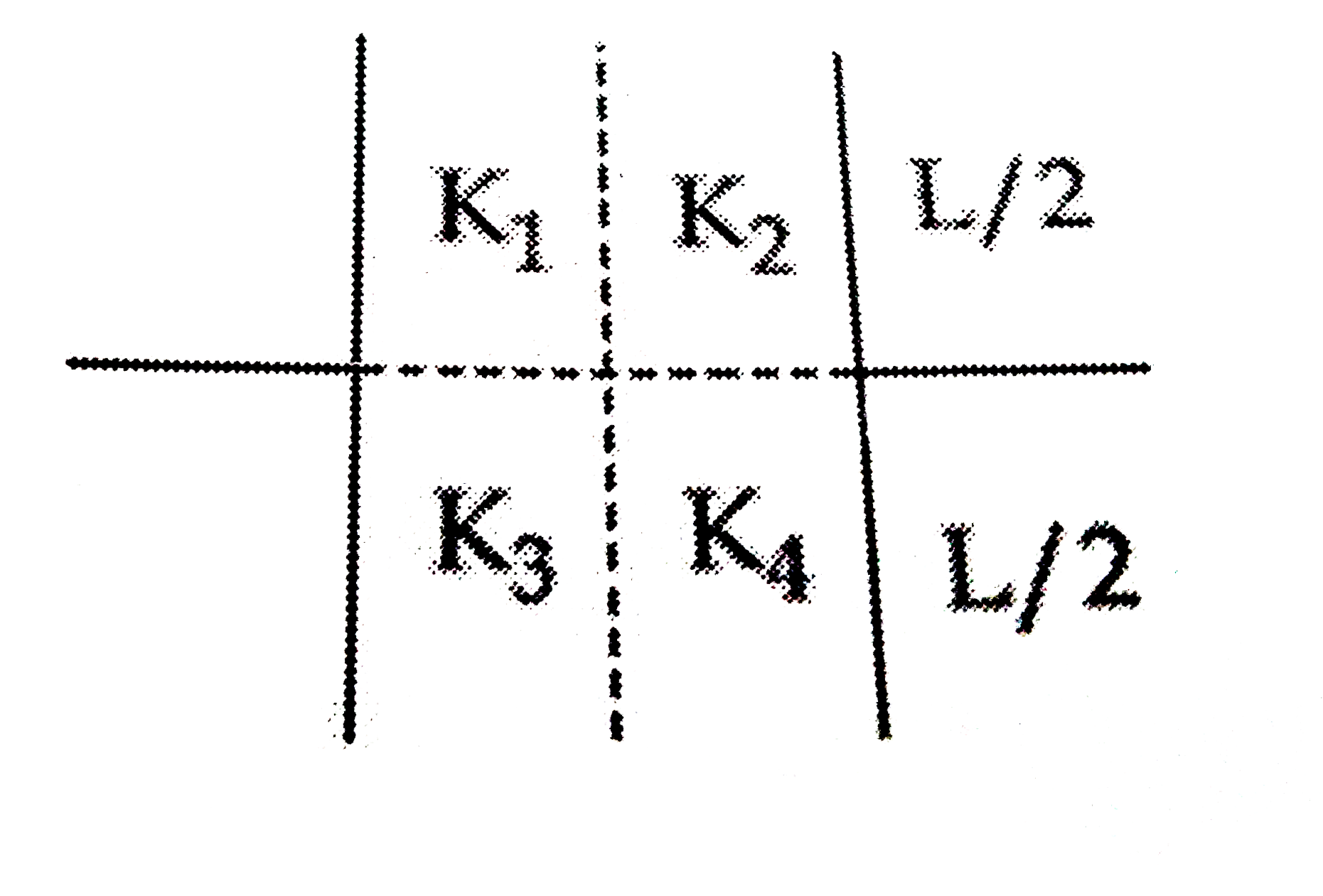 View Solution
View Solution

