To mop-clean a floor, a cleaning machine presses a circular mop of radius R vertically down with a total force F and rotates it with a constant angular speed about its axis. If the force F is distributed uniformly over the mop and the floor is , the torque, applied by the machine on the mop is : a) b) c) d)
The correct Answer is:A
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 29 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 29 (2020)EXERCISE - PHYSICS
25 Videos
- JEE MAIN REVISION TEST - 7|JEE - 2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 7|JEE - 2020EXERCISE - Physics (Section -2) (Numerical Value Type)
5 Videos
Similar Questions
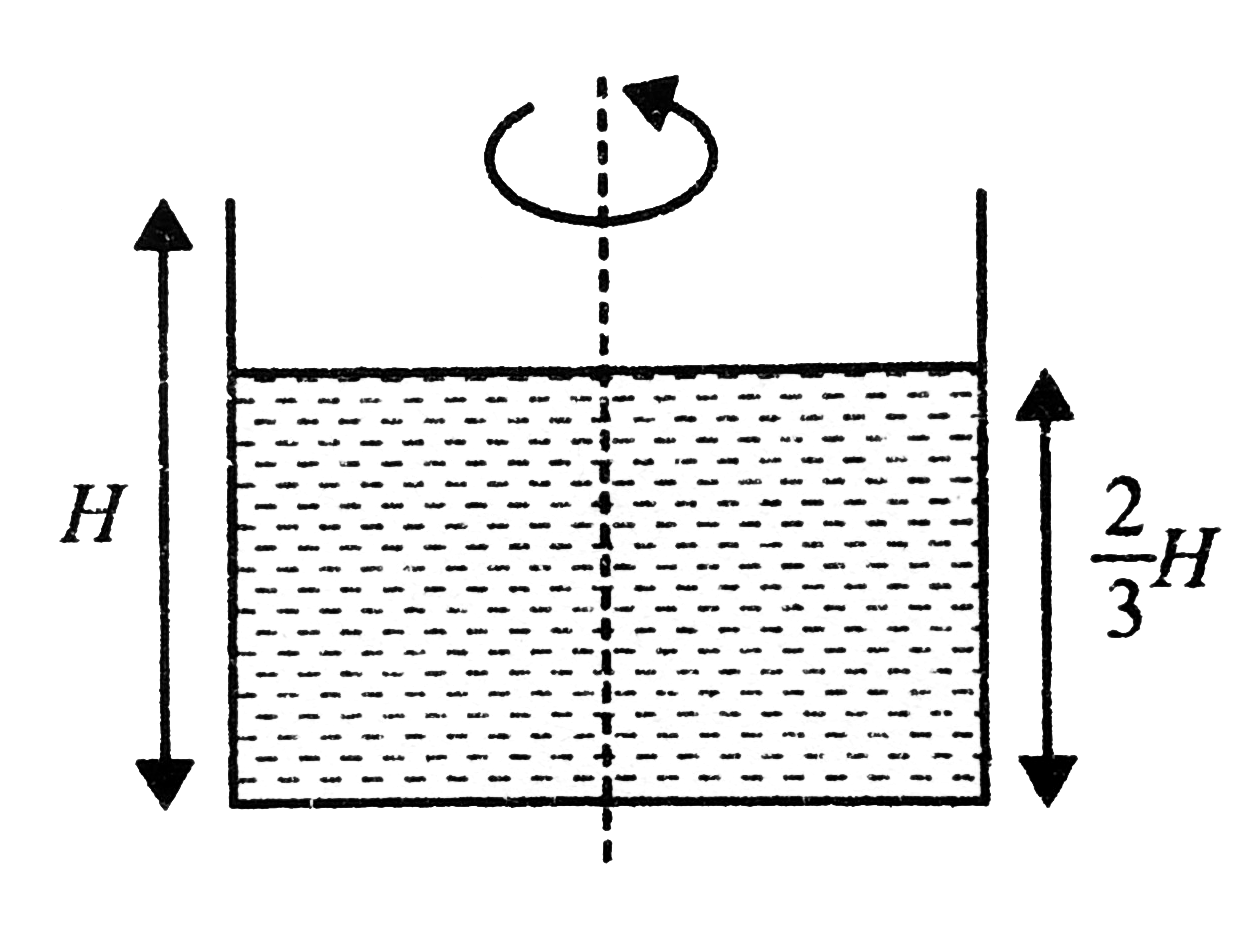
A circular cylinder of radius R and height H is filled with water to a height (2/3)H. It starts rotating about its axis with constantly increasing angular speed. Choose the correct alternatives.
View SolutionA thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
View Solution
Knowledge Check
A ballet dancer, dancing on a smooth floor is spinning about a vertical axis with her arms folded with angular velocity of 20rad/s. When the stretches her arms fully, the spinning speed decrease in 10rad/s. If I is the initial moment of inertia of the dancer, the new moment of inertia is: a) 2I b) 3I c) I/2 d) I/3
A2IB3ICI2DI3
A force →F=2ˆi+3ˆjN is applied to an object that is pivoted about a fixed axle aligned along the z coordinate axis. If the force is applied at the point →r=4ˆi+5ˆjm, (a) the magnitude of the net torque about the z and (b) the direction of the torque vector τ.
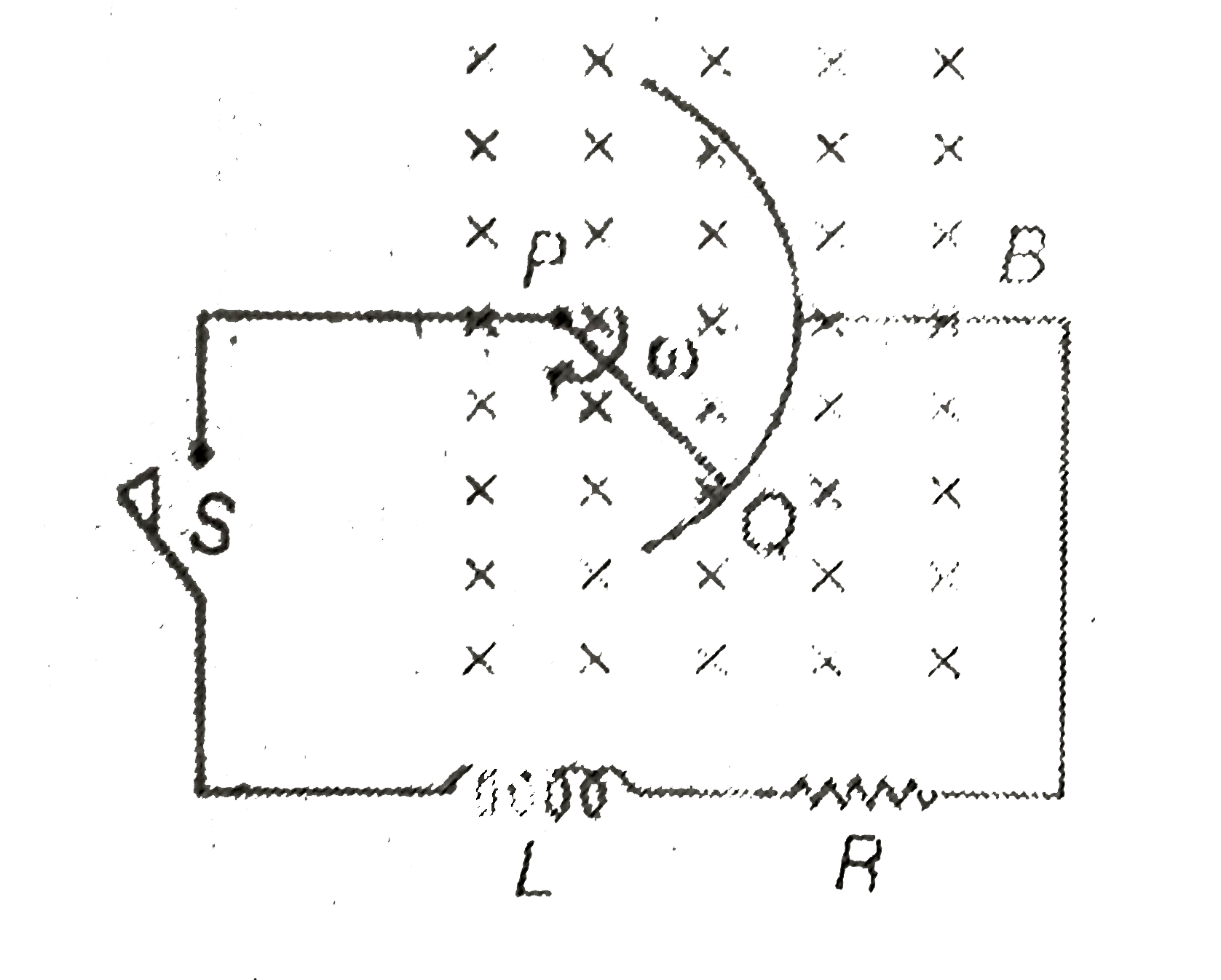
View SolutionThe circuit shows a resistance, R=0.01Ω and inductance L=3mH connected to a conducting rod PQ of length l=1m which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuit is seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity ω=2rad/sec. Find the magnitude of this torque (inN-m) at t=(0.3In 2) second.
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
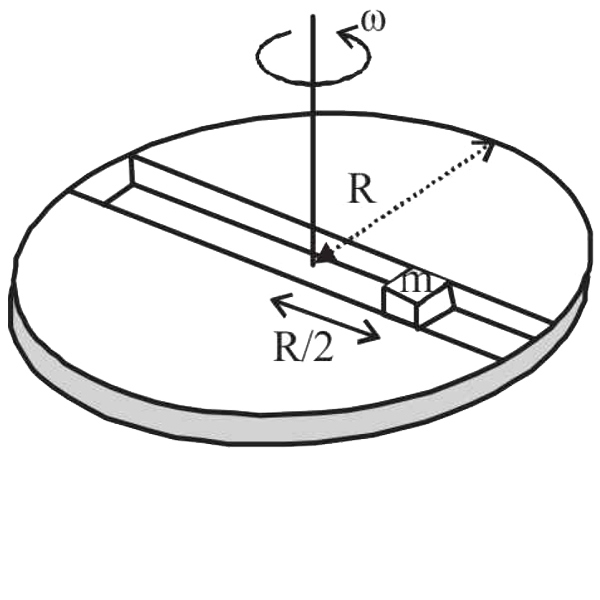
The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
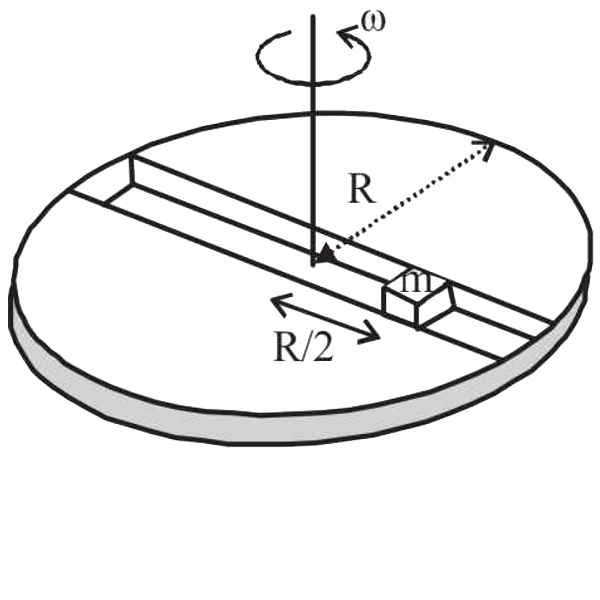
The net reaction of the disc on the block is
View SolutionA charge of (3.14×10−6) C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rad s^-1 . Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
View SolutionA rod of mass m can rotate without friction about axis sliding (also without friction) along a conducting ring of radius b arranged in a vertical plane as shown in the . The entire arrengement is placed in a uniform magnetic field with the inducetion B perpendicular to the plane of the ring. The axis and the conductor are connected to teh terminals of a current source. Determine
(a) according to which law current I flowing in the rod must vary for the rod to rotate at a constant angular speed. Being to measure the time from the instant when the rod is in its right-hand horizontal position. Consider the current to be positive when it flows from the axis of rotation toward the ring.
(b) what emf E of the source must be applied to maintain the required current? Consider the total resistance of the circuit to be constant and equal to R. Disergard the inductance of teh circuit.

View SolutionThree particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View Solution

