Water flows into a large tank with flat bottom at the rate of 10−4m3s−1. Water is also leaking out of a hole of area 1 cm2 at its bottom. If the height of the water in the tank remains steady, then this height is :
2.9 cm
1.7 cm
4 cm
5.1 cm
The correct Answer is:D
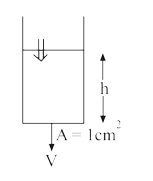
10−4=10−4×V
⇒V=1 m/s
pgh =12pV2
V=√2gh⇒h=V22g=12×9.8=5.1 cm
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 29 (2020)EXERCISE - PHYSICS25videos
JEE MAIN REVISION TEST - 29 (2020)
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 7|JEE - 2020EXERCISE - Physics (Section -2) (Numerical Value Type)5videos
JEE MAIN REVISION TEST - 7|JEE - 2020
Similar Questions
The level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
View SolutionA cylindrical tank whose cross-section area is 2000cm2 has a hole in its bottom 1cm2 in area.
(i) If the water is allowed to flow into the tank from a tube above it at the rate of 140 cm3/s, how high will the water in the tank rise ?
(ii) If the flow of water into the tank is stopped after the above height has been reached, how long will it take for tank to empty itself through the hole?View Solution
Knowledge Check
- Question 1 - Select One
A tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)
Water is dripping out from a conical funnel of semi-vertical angle π4 at the uniform rate of 2cm3/sec in its surface area through a tiny hole at the vertex in the bottom. When the slant height of the water is 4cm, find the rate of decrease of the slant height of the water.
View SolutionWater is dripping out from a conical funnel of semi-vertical angle π4 at the uniform rate of 2cm3/sec in its surface area through a tiny hole at the vertex in the bottom. When the slant height of the water is 4cm, find the rate of decrease of the slant height of the water.
View SolutionWater is being poured in a vessel at a constant rate αm2/s. There is a small hole of area a at the bottom of the tank. The maximum level of water in the vessel is proportional to
View SolutionWater is dripping out from a conical funnel at a uniform rate of 4cm3/cm through a tiny hole at the vertex in the bottom. When the slant height of the water is 3cm, find the rate of decrease of the slant height of the water-cone. Given that the vertical angle of the funnel is 1200.
View SolutionWater is dripping out from a conical funnel at a uniform rate of 4cm3/cm through a tiny hole at the vertex in the bottom. When the slant height of the water is 3cm, find the rate of decrease of the slant height of the water-cone. Given that the vertical angle of the funnel is 1200.
View SolutionWater is dripping out from a conical funnel of semi-vertical angle π4 at the uniform rate of 2cm2/sec in the surface through a tiny hole at the vertex of the bottom. When the slant height of the water level is 4 cm, find the rate of decrease of the slant heights of the water.
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is oured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.
View Solution

