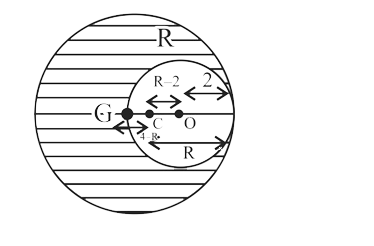
As shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
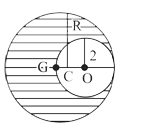
(R2−2R+4)(4−R)=8
(R2+2R−4)(4−R)=8
(R2+2R+4)(4−4)=8
(R2−2R−4)(4−R)=8
The correct Answer is:C
By concept of COM
m1R1=m2R2
Remaining mass × (4-R) = Cavity mass ×(R-2)
(43πR2ρ−43π23ρ)(4−R)=43π23ρ×(R×2)
(R2+2R+4)(4−R)=8
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 27 - JEE -2020EXERCISE - PHYSICS (SECTION 2)5videos
JEE MAIN REVISION TEST - 27 - JEE -2020
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 26 (2020)EXERCISE - PHYSICS (SECTION 2)5videos
JEE MAIN REVISION TEST - 26 (2020)
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 28EXERCISE - PHYSICS (SECTION-2)5videos
JEE MAIN REVISION TEST - 28
Similar Questions
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is
 View Solution
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 View Solution
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 View Solution
View SolutionA uniform metal disck of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View SolutionFrom a circular disc of radius R a square is cut out with a radius as its diagonal . The distane of the centre of mass of the remainder from the centre of the disc is
View Solution_E01_017_Q01.png)
A spherical cave of radius R/2 was carved out from a uniform sphere of radius R and original mass M. the center of the cave is at R/2 from the center of the large sphere. Point P is at a distance 2R from the center the large sphere and on the joing line of the two centers. the gravitational field strength g at point P isView SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 View Solution
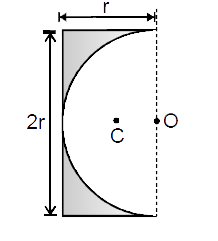
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
 View Solution
View SolutionThe radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point R2 away from the centre of the sphere is:
View Solution

