Within a spherical charge distribution of charge density , N equipotential surface of potential , are drawn and have increasing radii , respectively. If the difference in the radii of the surface is constant for all values of and then :-
(a) = constant
(b)
(c)
(d)
The correct Answer is:C
To solve the problem, we will analyze the spherical charge distribution and the relationship between the potential and the radius of the equipotential surfaces.
1. Understanding the Problem:
We have a spherical charge distribution with a charge density ρ(r). There are N equipotential surfaces with potentials V0,V0+ΔV,V0+2ΔV,…,V0+NΔV and corresponding radii r0,r1,r2,…,rN. The difference in the radii of these surfaces is constant.
2. Applying Gauss's Law:
To analyze the electric field E due to a spherical charge distribution, we can use Gauss's Law:
Φ=∮E⋅dA=Qencϵ0
For a spherical surface of radius r:
E⋅4πr2=Qencϵ0
where Qenc is the charge enclosed within radius r.
3. Charge Enclosed:
The charge enclosed can be expressed as:
Qenc=∫r0ρ(r′)⋅4πr′2dr′
4. Relating Electric Field and Potential:
The electric field E is related to the potential V by:
E=−dVdr
Given that the potential difference ΔV is constant, we can write:
dVdr=constant
5. Finding the Relationship:
From the expression for E and using Gauss's law:
E=Qenc4πϵ0r2
Combining this with the relationship for the potential, we can derive:
dVdr=−Qenc4πϵ0r2
6. Density and Radius Relationship:
Since dVdr is constant, we can conclude that:
ρ(r)⋅r2 is constant
This leads us to:
ρ(r)∝1r
7. Conclusion:
The relationship between the charge density ρ and the radius r is given by:
ρ(r)∝1r
Thus, the correct option is (C).
We have a spherical charge distribution with a charge density ρ(r). There are N equipotential surfaces with potentials V0,V0+ΔV,V0+2ΔV,…,V0+NΔV and corresponding radii r0,r1,r2,…,rN. The difference in the radii of these surfaces is constant.
To analyze the electric field E due to a spherical charge distribution, we can use Gauss's Law:
Φ=∮E⋅dA=Qencϵ0
For a spherical surface of radius r:
E⋅4πr2=Qencϵ0
where Qenc is the charge enclosed within radius r.
The charge enclosed can be expressed as:
Qenc=∫r0ρ(r′)⋅4πr′2dr′
The electric field E is related to the potential V by:
E=−dVdr
Given that the potential difference ΔV is constant, we can write:
dVdr=constant
From the expression for E and using Gauss's law:
E=Qenc4πϵ0r2
Combining this with the relationship for the potential, we can derive:
dVdr=−Qenc4πϵ0r2
Since dVdr is constant, we can conclude that:
ρ(r)⋅r2 is constant
This leads us to:
ρ(r)∝1r
The relationship between the charge density ρ and the radius r is given by:
ρ(r)∝1r
Thus, the correct option is (C).
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 18EXERCISE - PHYSICS - SECTION 25videos
JEE MAIN REVISION TEST - 18
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 13EXERCISE - PHYSICS (SECTION 2)5videos
JEE MAIN REVISION TEST - 13
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 19EXERCISE - PHYSICS25videos
JEE MAIN REVISION TEST - 19
Similar Questions
Two planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
View SolutionA uniformly charged solid sphere of radius R has potential V0 (measured with respect to ∞) on its surface. For this sphere the equipotential surfaces with potentials 3V02,5V04,3V04 and V04 have radius R1,R2,R3 and R4 respecatively. Then
View Solution
Knowledge Check
- Question 1 - Select One
The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2
Two charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionThree capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .View Solution
.View SolutionA sphere of radius R has a variable charge density ρ(r)=ρ0rn−1(r≤R). If ratio of "potential at centre" and "potential at surface" be 3/2 then find the value of n
View SolutionGraph shows a hypothetical speed distribution for a sample of N gas particle (for V>V0,dNdV=0)
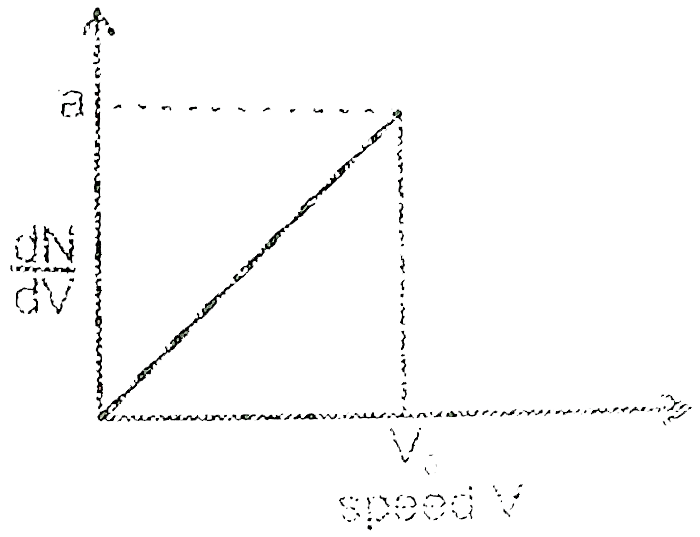 View Solution
View SolutionFor spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0
 View Solution
View SolutionA spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
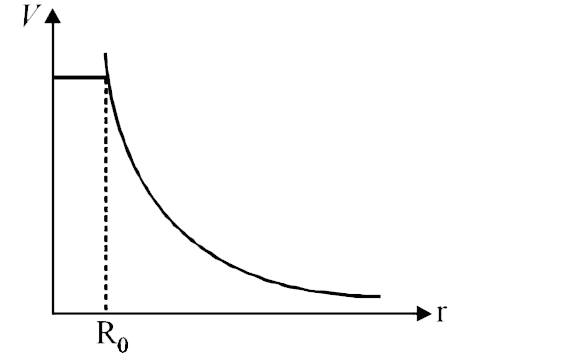 View Solution
View SolutionThree charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
View Solution

