let the point B be the reflection of the point A(2,3) with respect to the line 8x-6y-23=0. let TA and TB be circles of radii 2 and 1 with centres A and B respectively. Let T be a common tangent to the circles TA and TB such that both the circles are on the same side of T. if C is the point of intersection of T and the line passing through A and B then the length of the line segment AC is
The correct Answer is:10
To solve the problem step by step, we will follow these procedures:
Step 1: Find the reflection point B of point A(2, 3) with respect to the line 8x - 6y - 23 = 0.
1. Equation of the line: The line is given as 8x−6y−23=0.
2. Normal vector: The normal vector of the line can be derived from the coefficients of x and y, which gives us the vector →n=(8,−6).
3. Point A: The coordinates of point A are (2,3).
4. Distance from A to the line: The distance d from point A to the line can be calculated using the formula:
d=|8(2)−6(3)−23|√82+(−6)2=|16−18−23|√64+36=|−25|10=2.5
5. Projection of A onto the line: The coordinates of the foot of the perpendicular from A to the line can be calculated using the formula:
P=A−d√82+(−6)2⋅→n
Substituting the values:
P=(2,3)−2.510⋅(8,−6)=(2,3)−(2,−1.5)=(0,4.5)
6. Finding B: The reflection point B can be found as:
B=P+(P−A)=(0,4.5)+(0−2,4.5−3)=(0−2,4.5−3)=(−2,1.5)
Step 2: Define the circles TA and TB.
1. Circle TA: Center A(2, 3) with radius 2.
2. Circle TB: Center B(-2, 1.5) with radius 1.
Step 3: Find the equation of the line AB.
1. Slope of line AB: The slope m can be calculated as:
m=yB−yAxB−xA=1.5−3−2−2=−1.5−4=38
2. Equation of line AB: Using point-slope form:
y−3=38(x−2)⟹y=38x+218
Step 4: Find the common tangent T to the circles TA and TB.
1. Distance between centers A and B:
d=√(2−(−2))2+(3−1.5)2=√(4)2+(1.5)2=√16+2.25=√18.25
2. Using the formula for the length of the tangent:
L=√d2−(rA+rB)2=√18.25−(2+1)2=√18.25−9=√9.25
Step 5: Find the point of intersection C of the tangent T with line AB.
1. Using the tangent slope: The slope of the tangent line can be derived from the circles' properties.
2. Finding intersection point: Solve the system of equations formed by the tangent line and line AB.
Step 6: Calculate the length of segment AC.
1. Using distance formula:
AC=√(xC−2)2+(yC−3)2
Conclusion
After calculating the above steps, we find that the length of the line segment AC is 10 units.
2. Normal vector: The normal vector of the line can be derived from the coefficients of x and y, which gives us the vector →n=(8,−6).
3. Point A: The coordinates of point A are (2,3).
4. Distance from A to the line: The distance d from point A to the line can be calculated using the formula:
d=|8(2)−6(3)−23|√82+(−6)2=|16−18−23|√64+36=|−25|10=2.5
5. Projection of A onto the line: The coordinates of the foot of the perpendicular from A to the line can be calculated using the formula:
P=A−d√82+(−6)2⋅→n
Substituting the values:
P=(2,3)−2.510⋅(8,−6)=(2,3)−(2,−1.5)=(0,4.5)
6. Finding B: The reflection point B can be found as:
B=P+(P−A)=(0,4.5)+(0−2,4.5−3)=(0−2,4.5−3)=(−2,1.5)
2. Circle TB: Center B(-2, 1.5) with radius 1.
m=yB−yAxB−xA=1.5−3−2−2=−1.5−4=38
2. Equation of line AB: Using point-slope form:
y−3=38(x−2)⟹y=38x+218
d=√(2−(−2))2+(3−1.5)2=√(4)2+(1.5)2=√16+2.25=√18.25
2. Using the formula for the length of the tangent:
L=√d2−(rA+rB)2=√18.25−(2+1)2=√18.25−9=√9.25
2. Finding intersection point: Solve the system of equations formed by the tangent line and line AB.
AC=√(xC−2)2+(yC−3)2
Topper's Solved these Questions
Similar Questions
The point of intersection of the tangents at t1 and t2 to the parabola y2=12x is
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionThe length of the transversal common tangent to the circle x2+y2=1 and (x−t)2+y2=1 is √21, then t=
View SolutionThe reflection of the point (t−1,2t+2) in a line is (2t+1,t), then the equation of the line has slope equals to
View SolutionA, B, C are respectively the points (1,2), (4, 2), (4, 5). If T1,T2 are the points of trisection of the line segment BC, the area of the Triangle AT1T2 is
View SolutionA tangent to the ellipse 4x2+9y2=36 is cut by the tangent at the extremities of the major axis at T and T1, the circle on TT1 as diameter passes through the point
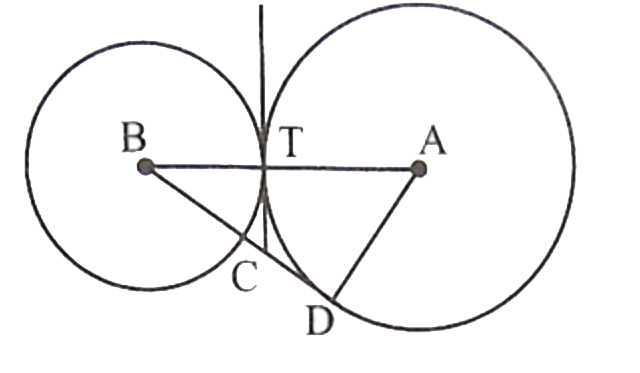
View SolutionTwo circles with centres at A and B touch each other externally at T. Let BD is the tangent at D and TC is a common tangent. If AT has length 3 units and BT has length 2 units, then the length (in units ) of CD is
View SolutionThe polars of points (1,7) (2,6) and (t,5) with respect to a circle concurrent then t=
View SolutionA circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
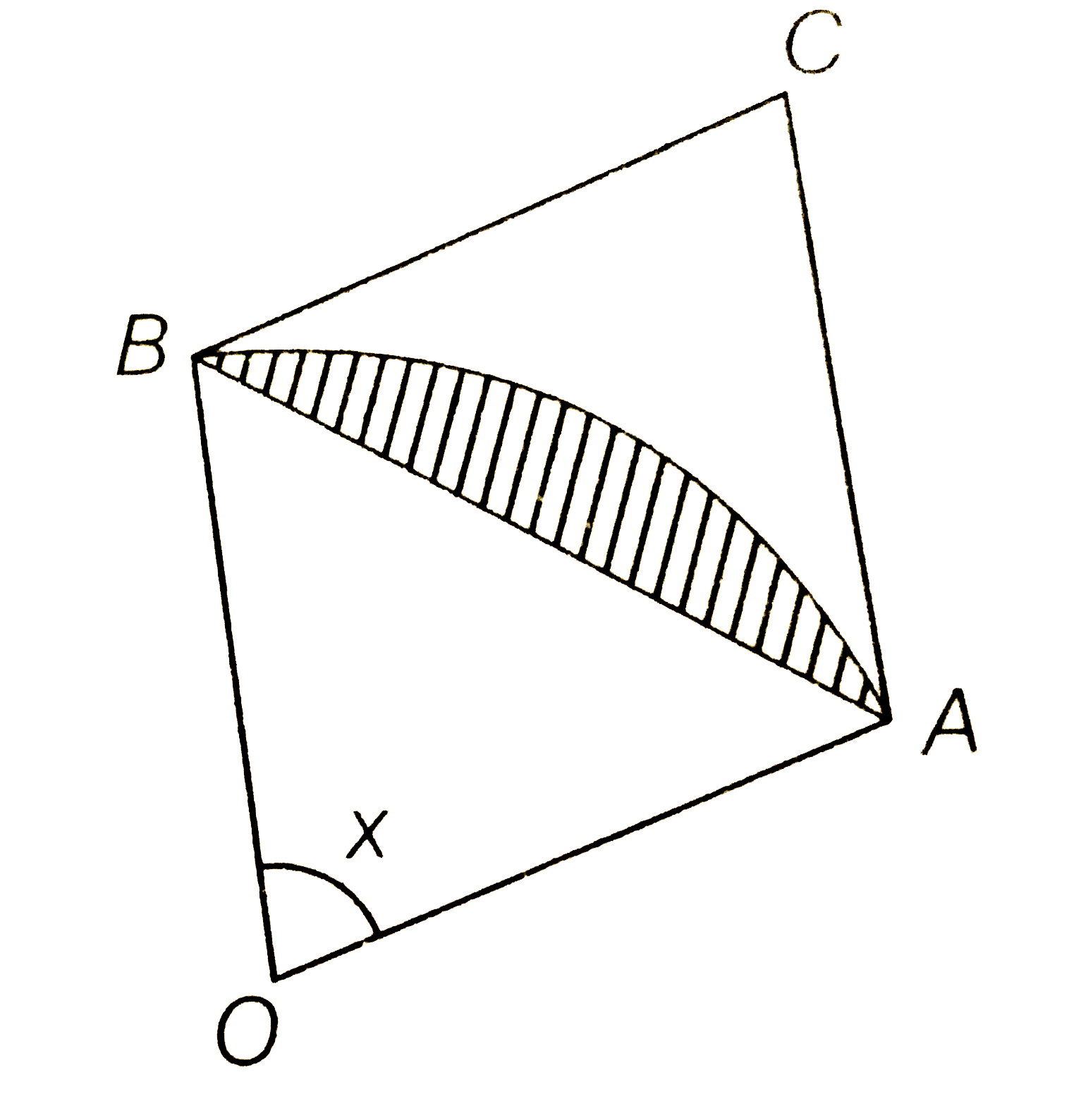
limx→0S(x)x is
View SolutionFind the equations of the tangent and the normal at the point 't' on the curve x=a sin3t , y=b cos3t .
View Solution
