The reflection of the point (t−1,2t+2) in a line is (2t+1,t), then the equation of the line has slope equals to
−1
1
12
0
The correct Answer is:B
To find the slope of the line given the reflection of the point (t−1,2t+2) is (2t+1,t), we can follow these steps:
Step 1: Identify the Points
Let point A be (t−1,2t+2) and point B be (2t+1,t).
Step 2: Find the Slope of Line AB
The slope m2 of line segment AB can be calculated using the formula:
m2=y2−y1x2−x1
Substituting the coordinates of points A and B:
- x1=t−1, y1=2t+2
- x2=2t+1, y2=t
So,
m2=t−(2t+2)(2t+1)−(t−1)
Step 3: Simplify the Slope Calculation
Calculating the numerator:
t−(2t+2)=t−2t−2=−t−2
Calculating the denominator:
(2t+1)−(t−1)=2t+1−t+1=t+2
Thus, the slope m2 becomes:
m2=−t−2t+2
Step 4: Relationship Between Slopes
Since line AB is perpendicular to line L (the line of reflection), we have:
m1⋅m2=−1
where m1 is the slope of line L.
Step 5: Substitute and Solve for m1
Substituting m2 into the equation:
m1⋅−t−2t+2=−1
Rearranging gives:
m1=−1⋅(t+2)−t−2=t+2t+2=1
Conclusion
Thus, the slope of the line L is:
1
Let point A be (t−1,2t+2) and point B be (2t+1,t).
The slope m2 of line segment AB can be calculated using the formula:
m2=y2−y1x2−x1
Substituting the coordinates of points A and B:
- x1=t−1, y1=2t+2
- x2=2t+1, y2=t
m2=t−(2t+2)(2t+1)−(t−1)
Calculating the numerator:
t−(2t+2)=t−2t−2=−t−2
(2t+1)−(t−1)=2t+1−t+1=t+2
m2=−t−2t+2
Since line AB is perpendicular to line L (the line of reflection), we have:
m1⋅m2=−1
where m1 is the slope of line L.
Substituting m2 into the equation:
m1⋅−t−2t+2=−1
m1=−1⋅(t+2)−t−2=t+2t+2=1
Thus, the slope of the line L is:
1
Similar Questions
Knowledge Check
- Question 1 - Select One
The parametric equation of a line are x=3-t and y=1+t. the slope of this line is
A−3B−1C−13D1
A, B, C are respectively the points (1,2), (4, 2), (4, 5). If T1,T2 are the points of trisection of the line segment BC, the area of the Triangle AT1T2 is
View Solutionlet the point B be the reflection of the point A(2,3) with respect to the line 8x-6y-23=0. let TA and TB be circles of radii 2 and 1 with centres A and B respectively. Let T be a common tangent to the circles TA and TB such that both the circles are on the same side of T. if C is the point of intersection of T and the line passing through A and B then the length of the line segment AC is
View SolutionThe coefficient of t50 in (1+t)41(1−t+t2)40 is equal to
View SolutionIf t=11−4√2 then t equals
View SolutionIf the normal to the rectangular hyperbola xy=c2 at the point 't' meets the curve again at t1 then t3t1, has the value equal to
View SolutionA line l passing through the origin is perpendicular to the lines
1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk−∞<t<∞and1_(2):(3+2s)ˆi+(3+2s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<s<∞
Then the coordinate(s) of the point(s) on 12 at a distance of √17 from the point of intersection of 1 and 11 is (are)View SolutionLine t is shown in the xy-plane below
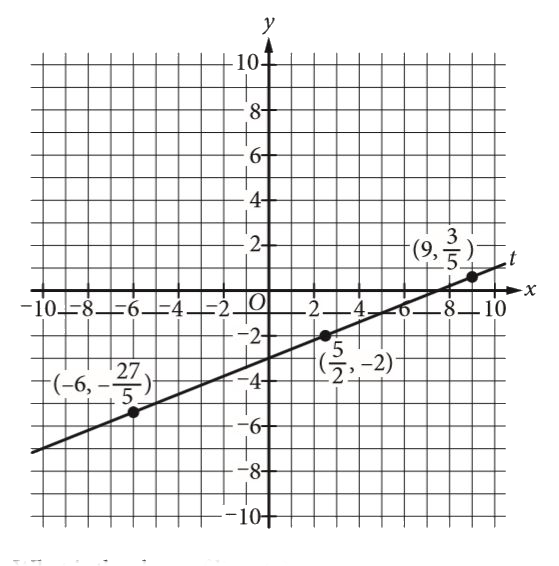
What is the slope of line t ?View Solution

