P is the probability of finding the 1s electron of hydrogen atom in a spherical shell of infinitesimal thickness dr, at a distance r from the nucleus. The volume of this shell is 4πr2dr. The qualitative sketch of the dependence of P or r is
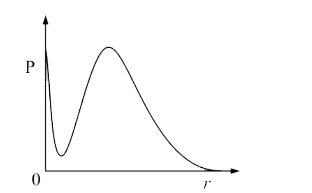

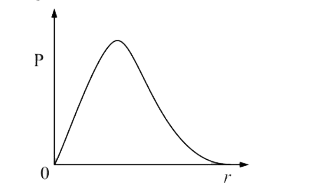
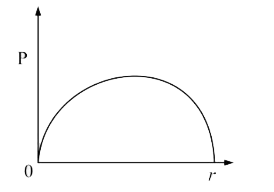
The correct Answer is:C
Radial nodes for 1s = 0.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - JEE Main (Archive)39videos
ATOMIC STRUCTURE
- BOOK - VMC MODULES ENGLISHCHAPTER - AMINESEXERCISE - IN CHAPTER EXERCISE H10videos
AMINES
- BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL BONDING & CHEMICAL STRUCTURE EXERCISE - IMPECCABLE50videos
CHEMICAL BONDING & CHEMICAL STRUCTURE
Similar Questions
The radial probability is the probability of finding electron in a small spherical shell around the nucleus at a particular distance r. Hence radial probability is
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View Solution
Knowledge Check
- Question 1 - Select One
P is the probability of finding the Is electron of hydrogen atom in a spherical shell of infitesimal thickness, dr, at a distance r from the nucleus. The volume of this shell is 4πr2dr. The qualitative sketch of the dependence of P on r is
A B
B C
C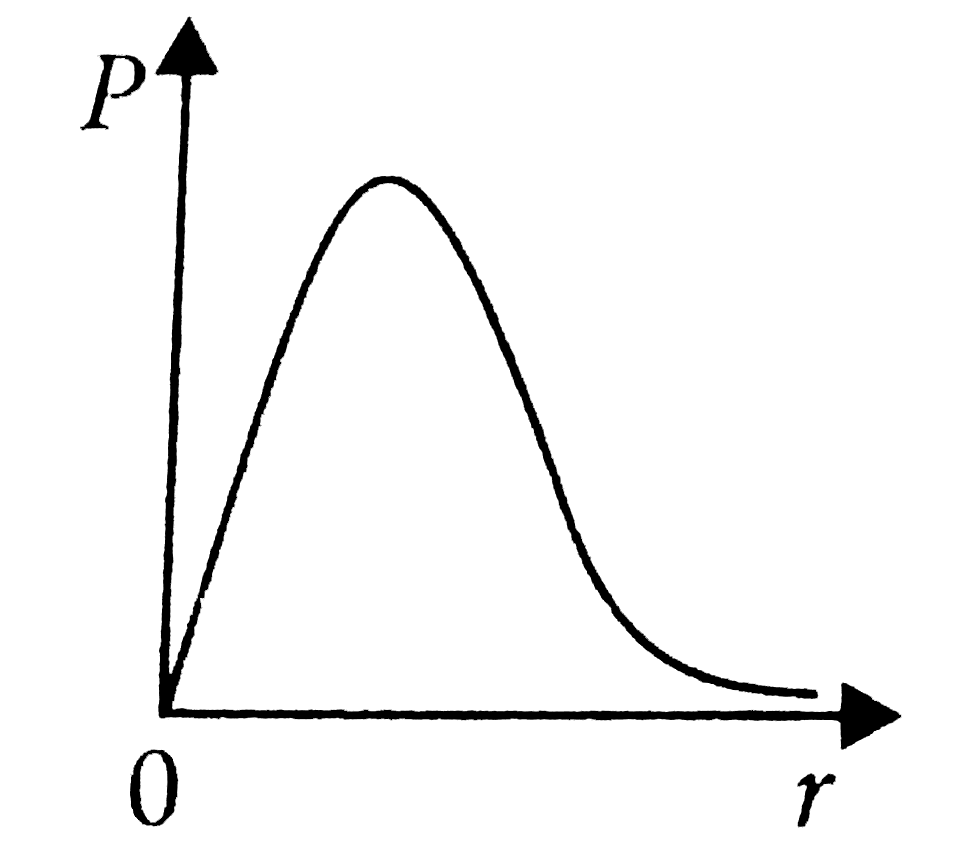 D
D
The electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionFor a given uniform spherical shell of mass M and radius R find gravitational field at a distancer r from centre in following two cases (a) r≥R (b) r<R .
View Solution
A point charge q'q is placed at distance 'a' from the centre of an uncharged thin spherical conducting shell of radius R=2a. A point 'P' is located at a distance 4a from the centre of the conducting shell as shown. The electric potential due to induced charge on the inner surface of the conducting shell at point 'P' isView SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
The graph of the radial component of E as function of r will beView SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R.The distance r<R.The electric potential at the centre of the shell will be
 View Solution
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be
 View Solution
View Solution

