The sum of these three vectors is :
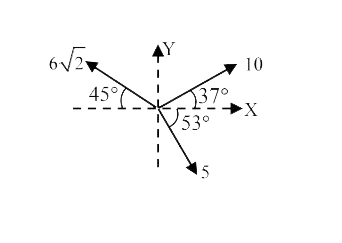
4ˆi+4ˆj
5ˆI−2ˆj
4ˆi+3ˆj
5ˆi+8ˆj
The correct Answer is:d
(10cos37ˆi+10sin37ˆj)+6√cos45(ˆi)+6√2sin45ˆj+(5cos53ˆi+53(ˆj)=(8ˆi+6ˆj)+(−6ˆi+6ˆj)+(3ˆi−4ˆj)=5ˆi+8ˆj)
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:level 2
Explore 65 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Main ( ARCHIVE ) ( LEVEL-1)
Explore 12 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART I : PHYSICS (SECTION - 2)
Explore 5 Videos
Similar Questions
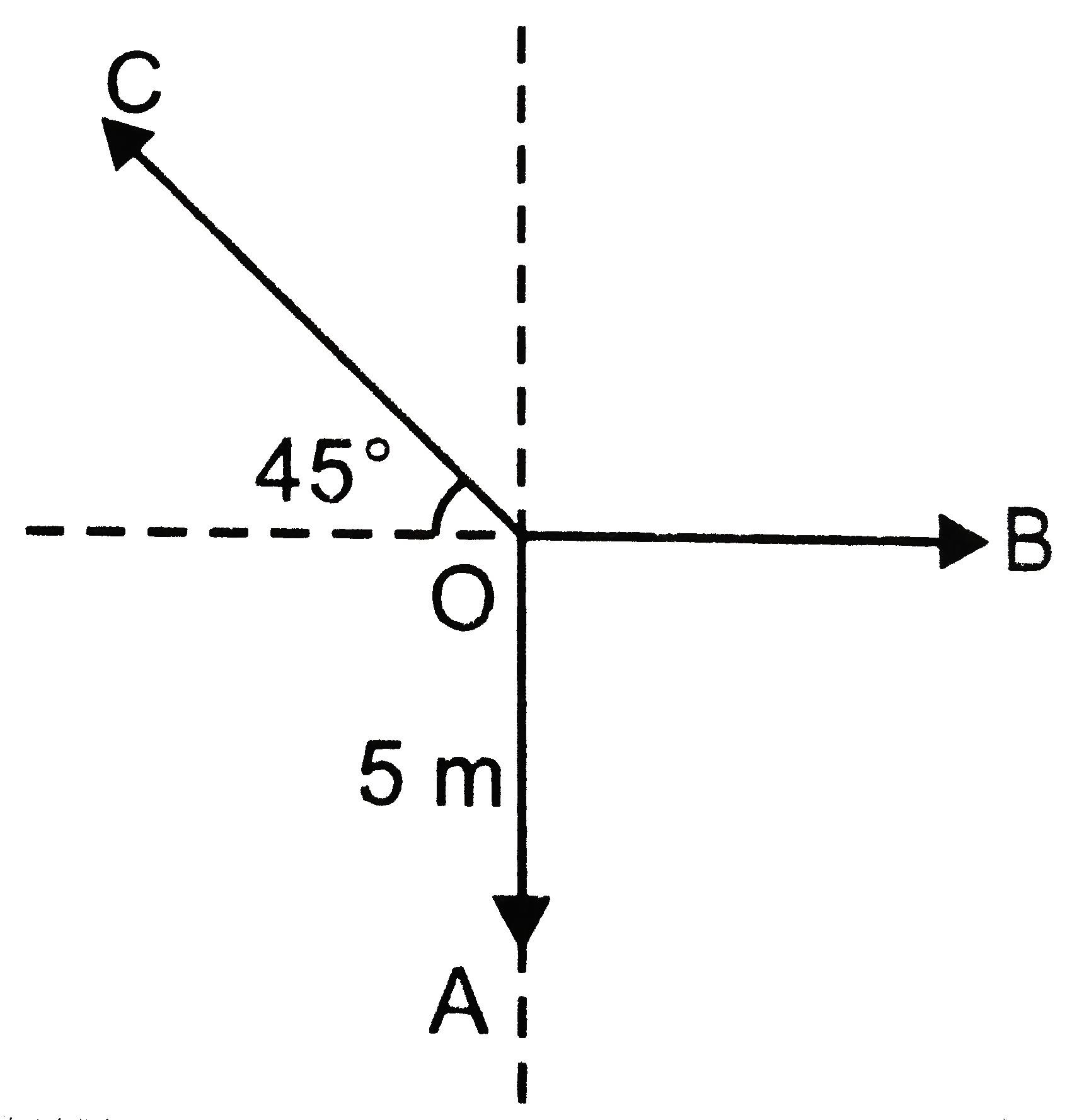
The sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.

View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?
View SolutionThree coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
View SolutionAn AP consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the last three terms is 429. Find the AP.
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
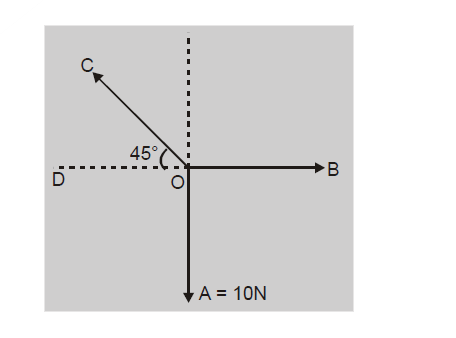
(ii) What is the magnitude of vector −−→OC ?
View SolutionFind the resultant of the three vectors shown in figure .
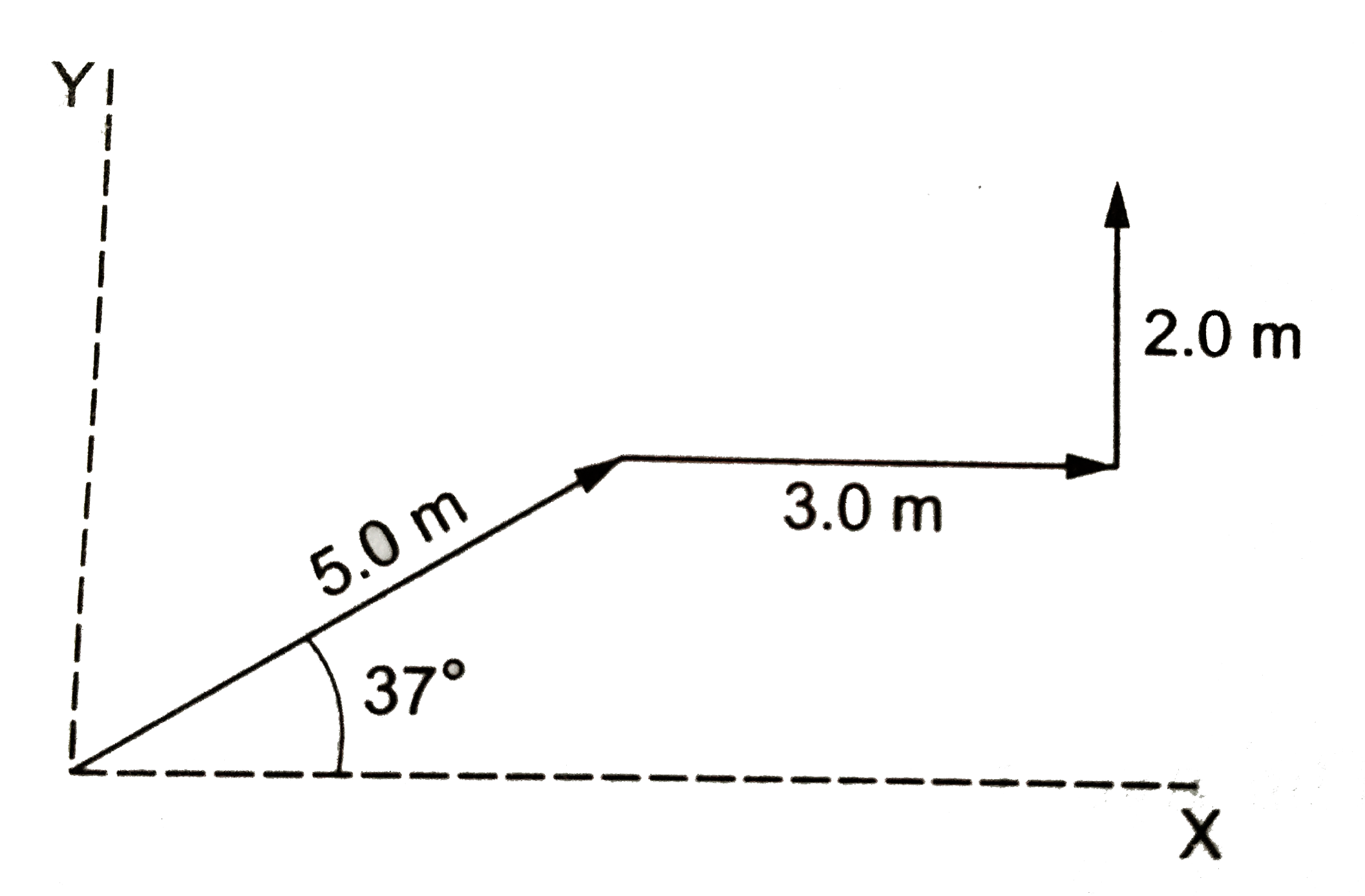 .
.
View SolutionThe sum of the first three terms of an arithmetic progression is 9 and the sum of their squares is 35. The sum of the first n terms of the series can be
View SolutionThe sum of the first three terms of an increasing G.P. is 21 and the sum of their squares is 189. Then the sum of its first n terms is
View SolutionThe sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the GP.
View SolutionThe sum of first three terms of a G.P is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the G.P.
View Solution
