Three coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
To solve the given problem, we need to find the resultant of three co-initial vectors of magnitudes a, 2a, and 3a that are directed along the diagonals of three adjacent faces of a cube. We will also prove that the sum of these vectors is twice the vector determined by the diagonal of the cube.
Step 1: Understanding the Cube and Vectors
Let's denote the cube's vertices as follows:
- O (origin)
- A (1, 0, 0)
- B (0, 1, 0)
- C (0, 0, 1)
The vectors along the diagonals of the three adjacent faces can be represented as:
- →OB along the face OAB
- →OC along the face OAC
- →OD along the face OBC
Step 2: Expressing the Vectors
We can express the vectors in terms of unit vectors:
- Let ^i be the unit vector along the x-axis.
- Let ^j be the unit vector along the y-axis.
- Let ^k be the unit vector along the z-axis.
The vectors can be expressed as:
- →OB=a(1√2^i+1√2^j)
- →OC=2a(1√2^j+1√2^k)
- →OD=3a(1√2^k+1√2^i)
Step 3: Finding the Resultant Vector
Now, we find the resultant vector →R by adding these three vectors:
→R=→OB+→OC+→OD
Substituting the expressions, we have:
→R=a(1√2^i+1√2^j)+2a(1√2^j+1√2^k)+3a(1√2^k+1√2^i)
Step 4: Simplifying the Resultant
Now, we can combine the terms:
→R=(a√2+3a√2)^i+(a√2+4a√2)^j+(2a√2+3a√2)^k
This simplifies to:
→R=4a√2^i+5a√2^j+5a√2^k
Step 5: Proving the Second Part
To prove that the sum of the three vectors is twice the vector determined by the diagonal of the cube, we need to find the vector along the diagonal of the cube:
- The diagonal vector →D of the cube can be represented as →D=a(^i+^j+^k).
Now, we find 2→D:
2→D=2a(^i+^j+^k)=2a^i+2a^j+2a^k
Conclusion
We have shown that the resultant vector →R is equal to 2→D, thus proving that the sum of the three vectors determined by the diagonals of the three adjacent faces of a cube passing through the same corner is twice the vector determined by the diagonal of the cube.
Let's denote the cube's vertices as follows:
- O (origin)
- A (1, 0, 0)
- B (0, 1, 0)
- C (0, 0, 1)
- →OB along the face OAB
- →OC along the face OAC
- →OD along the face OBC
We can express the vectors in terms of unit vectors:
- Let ^i be the unit vector along the x-axis.
- Let ^j be the unit vector along the y-axis.
- Let ^k be the unit vector along the z-axis.
- →OB=a(1√2^i+1√2^j)
- →OC=2a(1√2^j+1√2^k)
- →OD=3a(1√2^k+1√2^i)
Now, we find the resultant vector →R by adding these three vectors:
→R=→OB+→OC+→OD
Substituting the expressions, we have:
→R=a(1√2^i+1√2^j)+2a(1√2^j+1√2^k)+3a(1√2^k+1√2^i)
Now, we can combine the terms:
→R=(a√2+3a√2)^i+(a√2+4a√2)^j+(2a√2+3a√2)^k
This simplifies to:
→R=4a√2^i+5a√2^j+5a√2^k
To prove that the sum of the three vectors is twice the vector determined by the diagonal of the cube, we need to find the vector along the diagonal of the cube:
- The diagonal vector →D of the cube can be represented as →D=a(^i+^j+^k).
2→D=2a(^i+^j+^k)=2a^i+2a^j+2a^k
We have shown that the resultant vector →R is equal to 2→D, thus proving that the sum of the three vectors determined by the diagonals of the three adjacent faces of a cube passing through the same corner is twice the vector determined by the diagonal of the cube.
Topper's Solved these Questions
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type
6 Videos
- VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSBOOK - CENGAGE ENGLISHCHAPTER - VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSEXERCISE - DPP 2.4
20 Videos
Similar Questions
Three vectors of magnitude a,2a,3a meet in a point and their directions are along the diagonals of the adjacent faces of a cube. Determine their resultant.
View SolutionThe sum of these three vectors is :
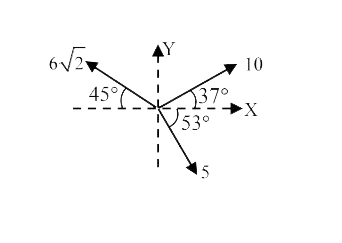
View SolutionProve that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionProve that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionShow that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionShow that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionThe areas of three adjacent faces of a cuboid are x, y and z. If the volume is V, prove that V2=xyz.
View SolutionFind the resultant of the three vectors shown in figure .
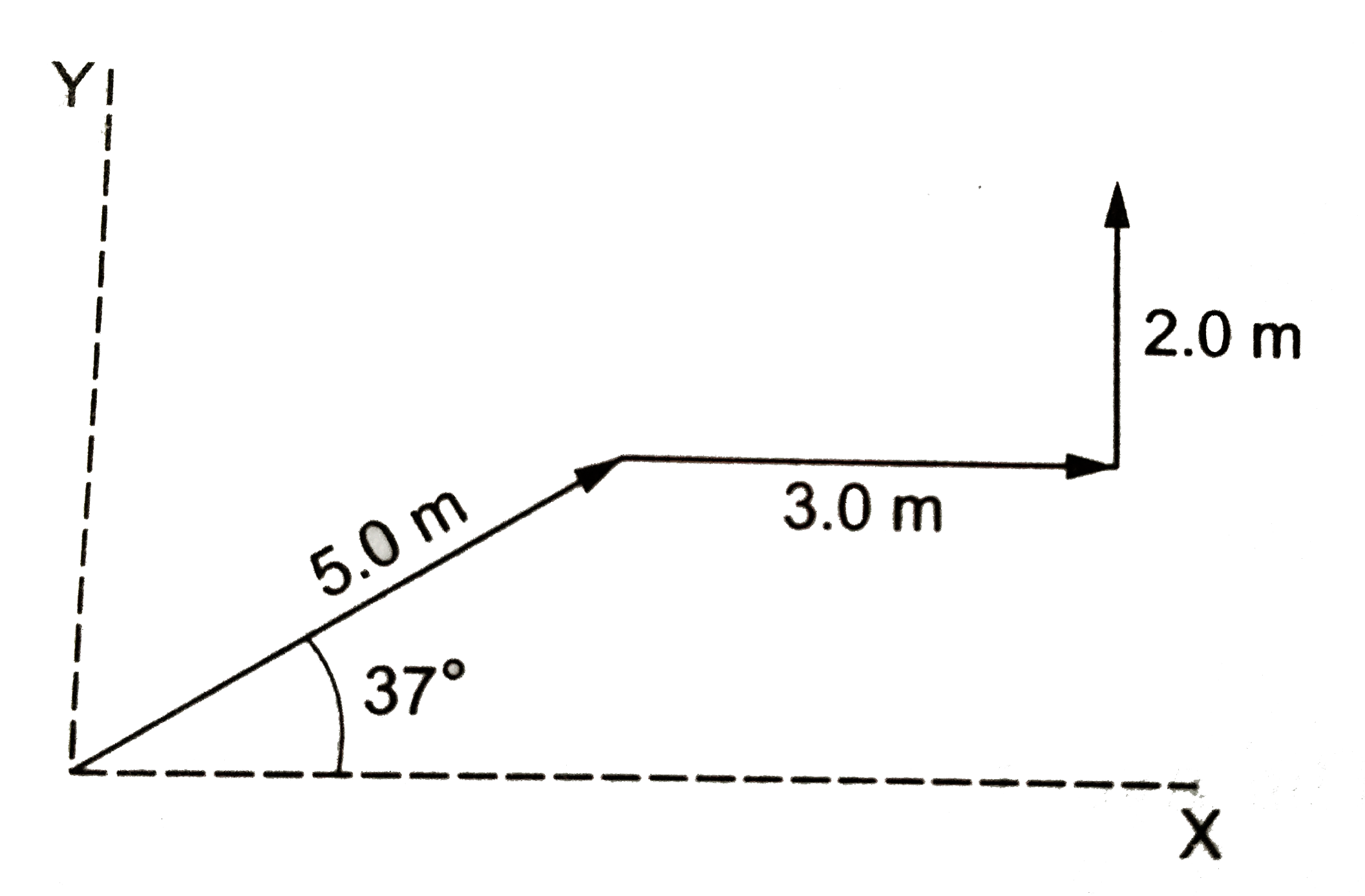 .
.
View SolutionFind the resultant of three vectors shown in the figure.
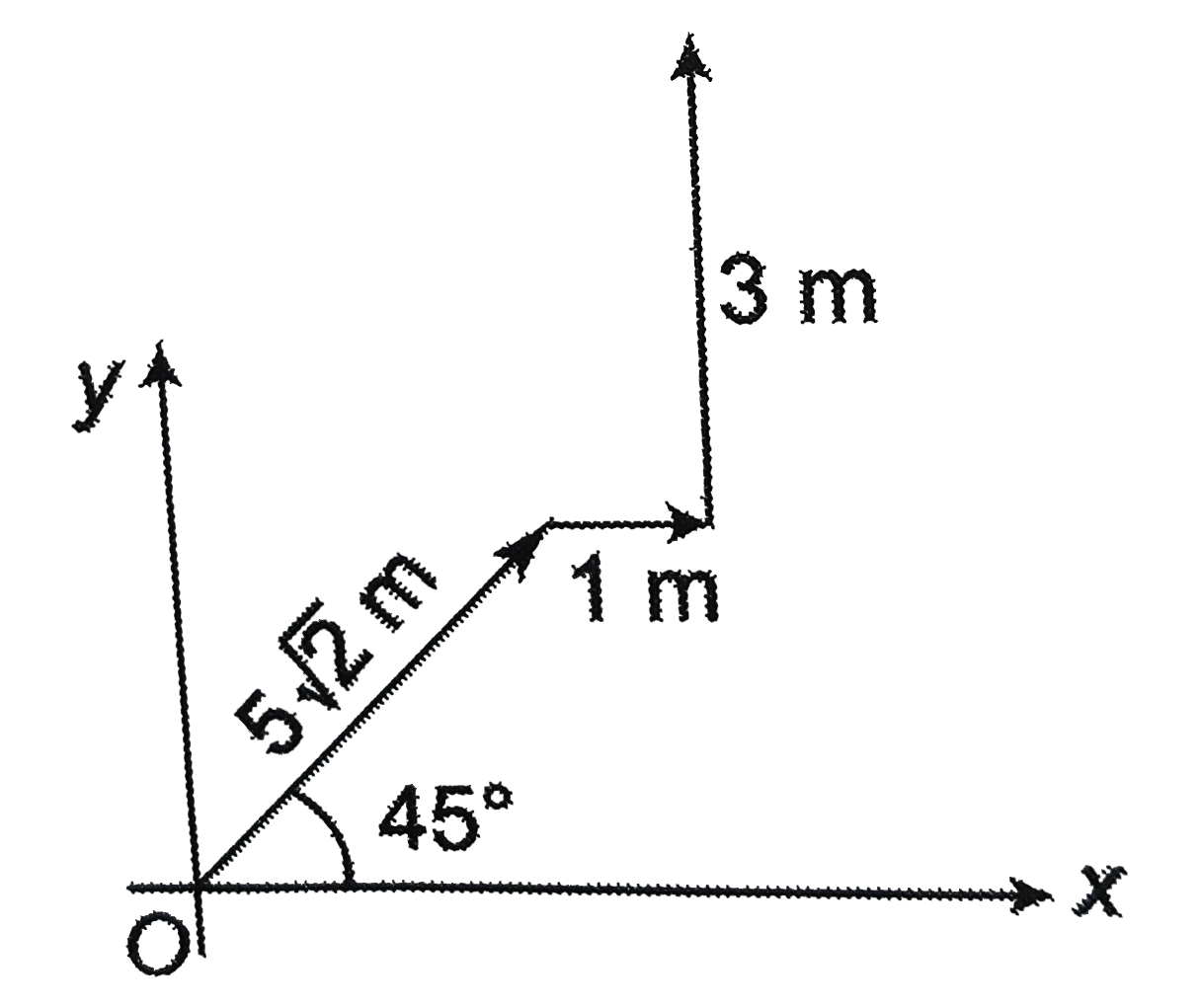
View SolutionThe angle between diagonal of a cube and diagonal
of a face of the cube will be
View Solution
