At the initial moment three points A, B and C are on a horizontal straight line at equal distances from one another. Point A begins to move vertically upward with a constant velocity v and point C vertically downward without any initial velocity but with a constant acceleration a. How should point B move vertically for all the three points to be constantly on one straight line. The points begin to move simultaneously.
acceleration a/2 and initial velocity v/2 both upwards
retardation a/2 and initial velocity v/2 both upwards
zero acceleration and initial velocity v
acceleration a/2 and initial velocity v both downwards
The correct Answer is:B
To solve the problem, we need to analyze the motion of points A, B, and C and ensure that they remain in a straight line as they move. Here’s a step-by-step solution:
Step 1: Define the Initial Positions
Let the initial positions of points A, B, and C be:
- A at (0, 0)
- B at (D, 0)
- C at (2D, 0)
Here, D is the distance between each point.
Step 2: Define the Motion of Points
- Point A moves vertically upward with a constant velocity v. Therefore, its position after time t will be:
A′=(0,vt)
- Point C moves vertically downward with an initial velocity of 0 and a constant acceleration a. Its position after time t will be:
C′=(2D,−12at2)
Step 3: Determine the Position of Point B
Let point B move vertically with an unknown velocity u and acceleration b. Its position after time t will be:
B′=(D,ut+12bt2)
Step 4: Ensure Collinearity of Points A, B, and C
For points A, B, and C to be collinear, the slopes of the lines connecting these points must be equal. We can use the concept of similar triangles.
The slope of line segment A′C′ is:
slopeA′C′=C′y−A′yC′x−A′x=−12at2−vt2D−0=−12at2−vt2D
The slope of line segment A′B′ is:
slopeA′B′=B′y−A′yB′x−A′x=ut+12bt2−vtD−0=ut+12bt2−vtD
Step 5: Set the Slopes Equal
For collinearity, set the two slopes equal:
−12at2−vt2D=ut+12bt2−vtD
Step 6: Simplify the Equation
Cross-multiplying gives:
−12at2−vt=2(ut+12bt2−vt)
Expanding and rearranging terms leads to:
−12at2−vt=2ut+bt2−2vt
−12at2+vt=2ut+bt2
Step 7: Solve for u and b
Rearranging gives:
vt+12at2=2ut+bt2
This can be rearranged to express u and b in terms of v and a:
u=v2andb=−a2
Conclusion
Thus, point B should move vertically with an initial velocity of v2 upwards and an acceleration of −a2 downwards.
Let the initial positions of points A, B, and C be:
- A at (0, 0)
- B at (D, 0)
- C at (2D, 0)
- Point A moves vertically upward with a constant velocity v. Therefore, its position after time t will be:
A′=(0,vt)
- Point C moves vertically downward with an initial velocity of 0 and a constant acceleration a. Its position after time t will be:
C′=(2D,−12at2)
Let point B move vertically with an unknown velocity u and acceleration b. Its position after time t will be:
B′=(D,ut+12bt2)
For points A, B, and C to be collinear, the slopes of the lines connecting these points must be equal. We can use the concept of similar triangles.
slopeA′C′=C′y−A′yC′x−A′x=−12at2−vt2D−0=−12at2−vt2D
slopeA′B′=B′y−A′yB′x−A′x=ut+12bt2−vtD−0=ut+12bt2−vtD
For collinearity, set the two slopes equal:
−12at2−vt2D=ut+12bt2−vtD
Cross-multiplying gives:
−12at2−vt=2(ut+12bt2−vt)
Expanding and rearranging terms leads to:
−12at2−vt=2ut+bt2−2vt
−12at2+vt=2ut+bt2
Rearranging gives:
vt+12at2=2ut+bt2
This can be rearranged to express u and b in terms of v and a:
u=v2andb=−a2
Thus, point B should move vertically with an initial velocity of v2 upwards and an acceleration of −a2 downwards.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)19videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)19videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Long Answer Type5videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J10videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K10videos
MOVING CHARGES & MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
A player throws a ball vertically upwards with velocity u. At highest point,
A1. both the velocity and acceleration of the ball are zero.B2. the velocity of the ball is u but its accelerationC3. the velocity of the ball is zero but its acceleration is g.D4. the velocity of the ball is u but its acceleration is g. - Question 2 - Select One
Two stones are thrown from the same point with velocity of 5 ms−1 one vertically upwards and the other vertically downwards. When the first stone is at the highest point the relative velocity of the second stone with respect to the first stone is,
A5ms−1B0ms−1C10ms−1D−5ms−1
Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionA particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
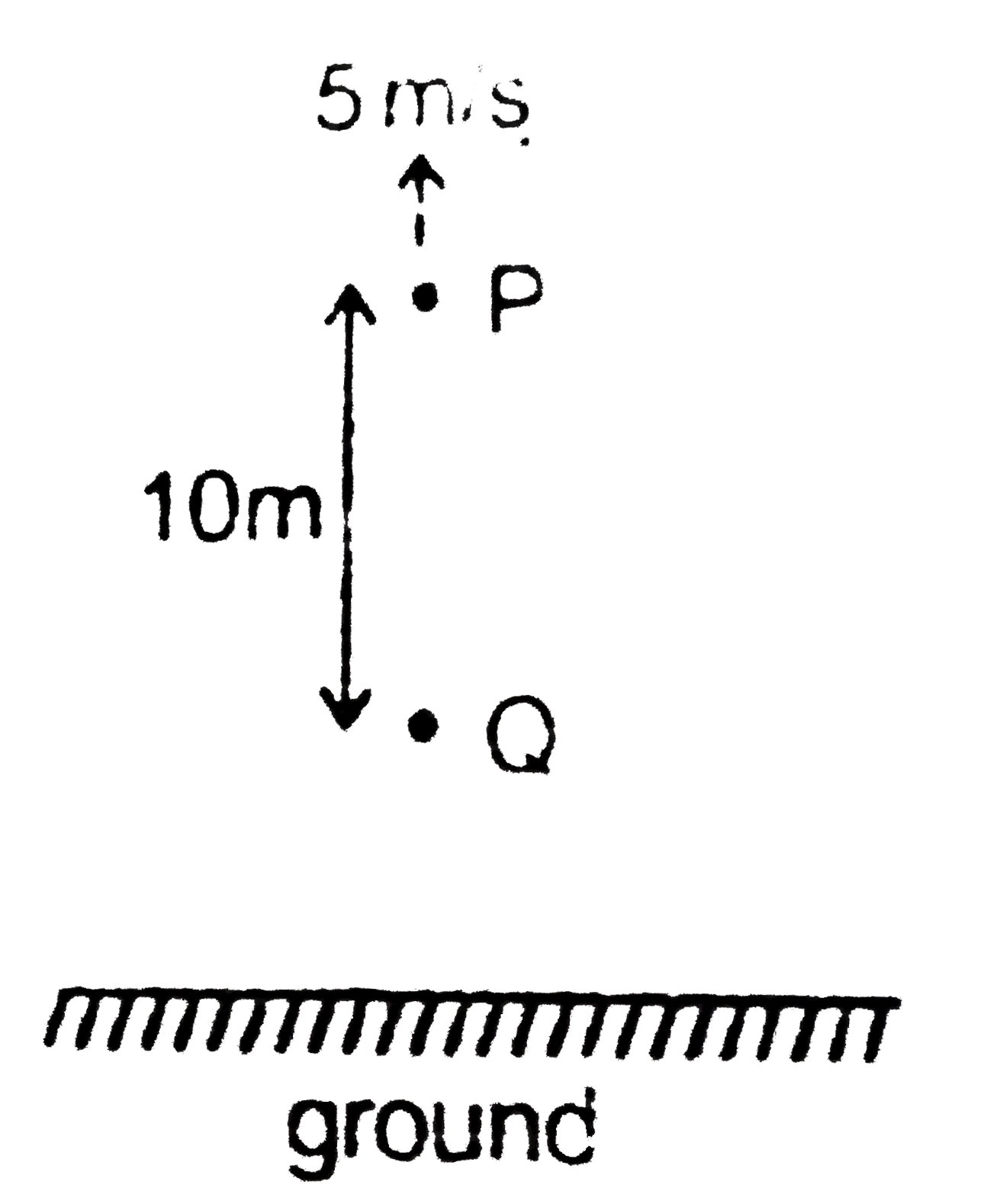
View SolutionA ball is thrown vertically upwards with an initial velocity of 5m/sec from point P as shown Q is a point 10m vertically below the point P. Then the speed of ball at point Q will be : (take g=10m/s2 and neglect air resistance)
 View Solution
View SolutionA stone is dropped freely while another thrown vertically downward with an initial velocity of 4 m/s from the same point simultaneously. The distance of separation between them will become 30 m after a time of
View SolutionFind the period of oscillation of a pendulum of length l if its point of suspension is
(a) moving vertically up with acceleration a
(b) moving vertically down with acceleration a(<g)
(c) failing freely under gravity
moving horizontal with acceleration a.View SolutionA particle P is projected with velocity u1 at an angle of 30∘ with the horizontal. Another particle Q is thrown vertically upwards with velocity u2 from a point vertically below the highest point of path of P. Determine the necessary condition for the two particles to collide at the highest point.
 .View Solution
.View Solution

