A ladder placed on a smooth floor slips. If at a given instant the velocity with which the ladder is slipping on the floor is v1, and the velocity of that part of ladder which is touching the wall is v1, then the velocity of the centre of the ladder at that instant is:
v1
v2
v1+v22
√v21+v222
The correct Answer is:D
To solve the problem of finding the velocity of the center of the ladder at the instant it is slipping, we can follow these steps:
Step 1: Understand the Setup
We have a ladder leaning against a wall and resting on a smooth floor. As the ladder slips, the point touching the floor moves with a velocity v1 horizontally, and the point touching the wall moves with a velocity v2 vertically downward.
Step 2: Define the Coordinates
Let's define the coordinates of the points:
- The point on the floor (bottom of the ladder) is at coordinates (x0,0).
- The point against the wall (top of the ladder) is at coordinates (0,y0).
- The center of the ladder will be at coordinates (x02,y02).
Step 3: Relate the Velocities
The velocity of the bottom point (slipping on the floor) is given as v1, and the velocity of the top point (slipping against the wall) is given as v2.
- The rate of change of x0 (horizontal position) is dx0dt=v1.
- The rate of change of y0 (vertical position) is dy0dt=−v2 (negative because it is moving downward).
Step 4: Calculate the Velocity of the Center of the Ladder
The velocity of the center of the ladder can be calculated by taking the average of the velocities of the two points:
- The velocity in the x-direction (horizontal) for the center is 12dx0dt=v12.
- The velocity in the y-direction (vertical) for the center is 12dy0dt=−v22.
Thus, the velocity of the center of the ladder can be expressed as:
→Vcenter=v12^i−v22^j
Step 5: Calculate the Magnitude of the Velocity
To find the magnitude of the velocity of the center of the ladder, we use the Pythagorean theorem:
|→Vcenter|=√(v12)2+(−v22)2
|→Vcenter|=√v214+v224=12√v21+v22
Final Answer
The velocity of the center of the ladder at that instant is:
12√v21+v22
We have a ladder leaning against a wall and resting on a smooth floor. As the ladder slips, the point touching the floor moves with a velocity v1 horizontally, and the point touching the wall moves with a velocity v2 vertically downward.
Let's define the coordinates of the points:
- The point on the floor (bottom of the ladder) is at coordinates (x0,0).
- The point against the wall (top of the ladder) is at coordinates (0,y0).
- The center of the ladder will be at coordinates (x02,y02).
The velocity of the bottom point (slipping on the floor) is given as v1, and the velocity of the top point (slipping against the wall) is given as v2.
- The rate of change of x0 (horizontal position) is dx0dt=v1.
- The rate of change of y0 (vertical position) is dy0dt=−v2 (negative because it is moving downward).
The velocity of the center of the ladder can be calculated by taking the average of the velocities of the two points:
- The velocity in the x-direction (horizontal) for the center is 12dx0dt=v12.
- The velocity in the y-direction (vertical) for the center is 12dy0dt=−v22.
→Vcenter=v12^i−v22^j
To find the magnitude of the velocity of the center of the ladder, we use the Pythagorean theorem:
|→Vcenter|=√(v12)2+(−v22)2
|→Vcenter|=√v214+v224=12√v21+v22
The velocity of the center of the ladder at that instant is:
12√v21+v22
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)19videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)19videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Long Answer Type5videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J10videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K10videos
MOVING CHARGES & MAGNETISM
Similar Questions
Velocity of the centre of a small cylinder is v. There is no slipping anywhere. The velocity of the centre of the larger cylinder is
 View Solution
View SolutionThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
 View Solution
View Solution
Due to slipping points A and B on the rim of the disk have the velocities shown. Determine the velocities of the centre point C and point F at this instant.View SolutionTwo partticles A and B intially at rest move towards each other under a mutual force of attraction. The instant at which velocity of A is 4v and velocity of B is 2v, the velocity of centre of mass of the system at that instant will be
View SolutionIf there is a moth sitting at point C of rolling sphere, where velocity of the centre of mass =v, calculate the velocity of the moth as seen by an oberver sitting at point D at this instant
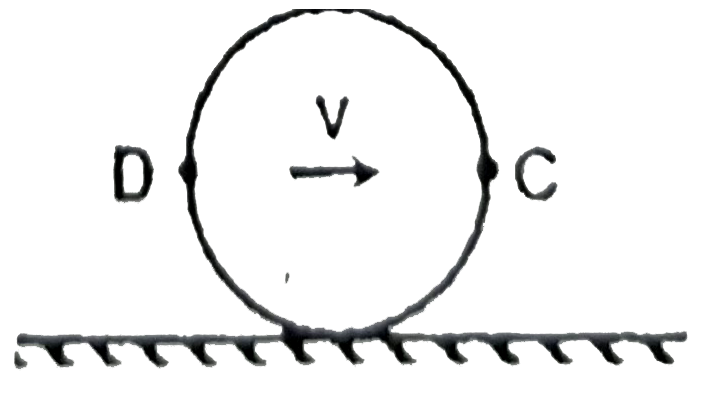 View Solution
View SolutionA thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View SolutionA hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA ladder 3.7 m long is placed against a wall in such a way that the foot of the ladder is 1.2 m away from the wall. Find the height of the wall to which the ladder reaches.
View SolutionA ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2m away from the wall and the ladder is making an angle of 60∘ with the level of the ground. Determine the height of the wall.
View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is
 View Solution
View Solution

