Match the entries of Column I and Column II.
COLUMN - I
(A) For a particle moving in a circle
(B) For a particle moving in a straight line
(C) For a particle undergoing projectile motion with the angle of projection α:0<α<π2
(D) For a particle moving in space
COLUMN - II
(P) The acceleration may be perpendicular to its velocity.
(Q) The acceleration may be in the direction of velocity
(R) The acceleration may be at some angle θ(0<θ<π2) with the velocity.
(S) The acceleration may be opposite to its velocity.
The correct Answer is:A-p, r; B-q, s; C-p, r; D=p,q r,s
To match the entries of Column I with Column II, we need to analyze each case in Column I and determine which statements from Column II are applicable.
Step 1: Analyze Column I Entry (A) - For a particle moving in a circle
- In uniform circular motion, the acceleration (centripetal acceleration) is directed towards the center of the circle, which is perpendicular to the velocity.
- Therefore, the matching entry is (P): The acceleration may be perpendicular to its velocity.
- In non-uniform circular motion, there can be tangential acceleration as well, which can create an angle with the velocity. Thus, the matching entry is also (R): The acceleration may be at some angle θ (where 0<θ<π/2) with the velocity.
- The acceleration cannot be in the direction of the velocity or opposite to it in uniform circular motion. Thus, entries (Q) and (S) are not applicable.
Conclusion for (A): Matches with (P) and (R).
---
Step 2: Analyze Column I Entry (B) - For a particle moving in a straight line
- If a particle is moving in a straight line, the acceleration can be in the same direction as the velocity, which corresponds to (Q): The acceleration may be in the direction of velocity.
- The acceleration cannot be perpendicular to the velocity, as this would cause the particle to move in a circular path. Therefore, (P) is not applicable.
- The acceleration can also be opposite to the velocity, which corresponds to (S): The acceleration may be opposite to its velocity (this is known as retardation).
- The acceleration cannot be at some angle with the velocity since the motion is constrained to a straight line. Thus, (R) is not applicable.
Conclusion for (B): Matches with (Q) and (S).
---
Step 3: Analyze Column I Entry (C) - For a particle undergoing projectile motion with angle of projection α:0<α<π/2
- At the highest point of projectile motion, the velocity is horizontal, and the acceleration due to gravity is vertical, making them perpendicular. Thus, it matches with (P): The acceleration may be perpendicular to its velocity.
- At any other point in the trajectory, the velocity and acceleration are not in the same direction, but they can form an angle θ (where 0<θ<π/2). Thus, it matches with (R): The acceleration may be at some angle θ with the velocity.
- The acceleration is never in the direction of the velocity or opposite to it during projectile motion. Thus, (Q) and (S) are not applicable.
Conclusion for (C): Matches with (P) and (R).
---
Step 4: Analyze Column I Entry (D) - For a particle moving in space
- In space, a particle can have acceleration in the direction of its velocity, matching with (Q): The acceleration may be in the direction of velocity.
- The acceleration can also be opposite to the velocity, matching with (S): The acceleration may be opposite to its velocity.
- The acceleration can be perpendicular to the velocity if the particle is given a sideways force, matching with (P): The acceleration may be perpendicular to its velocity.
- Additionally, the acceleration can be at some angle with the velocity, matching with (R): The acceleration may be at some angle θ with the velocity.
Conclusion for (D): Matches with (P), (Q), (R), and (S).
---
Final Matching:
- (A) → (P) and (R)
- (B) → (Q) and (S)
- (C) → (P) and (R)
- (D) → (P), (Q), (R), and (S)
- In uniform circular motion, the acceleration (centripetal acceleration) is directed towards the center of the circle, which is perpendicular to the velocity.
- Therefore, the matching entry is (P): The acceleration may be perpendicular to its velocity.
- In non-uniform circular motion, there can be tangential acceleration as well, which can create an angle with the velocity. Thus, the matching entry is also (R): The acceleration may be at some angle θ (where 0<θ<π/2) with the velocity.
- The acceleration cannot be in the direction of the velocity or opposite to it in uniform circular motion. Thus, entries (Q) and (S) are not applicable.
- If a particle is moving in a straight line, the acceleration can be in the same direction as the velocity, which corresponds to (Q): The acceleration may be in the direction of velocity.
- The acceleration cannot be perpendicular to the velocity, as this would cause the particle to move in a circular path. Therefore, (P) is not applicable.
- The acceleration can also be opposite to the velocity, which corresponds to (S): The acceleration may be opposite to its velocity (this is known as retardation).
- The acceleration cannot be at some angle with the velocity since the motion is constrained to a straight line. Thus, (R) is not applicable.
- At the highest point of projectile motion, the velocity is horizontal, and the acceleration due to gravity is vertical, making them perpendicular. Thus, it matches with (P): The acceleration may be perpendicular to its velocity.
- At any other point in the trajectory, the velocity and acceleration are not in the same direction, but they can form an angle θ (where 0<θ<π/2). Thus, it matches with (R): The acceleration may be at some angle θ with the velocity.
- The acceleration is never in the direction of the velocity or opposite to it during projectile motion. Thus, (Q) and (S) are not applicable.
- In space, a particle can have acceleration in the direction of its velocity, matching with (Q): The acceleration may be in the direction of velocity.
- The acceleration can also be opposite to the velocity, matching with (S): The acceleration may be opposite to its velocity.
- The acceleration can be perpendicular to the velocity if the particle is given a sideways force, matching with (P): The acceleration may be perpendicular to its velocity.
- Additionally, the acceleration can be at some angle with the velocity, matching with (R): The acceleration may be at some angle θ with the velocity.
- (A) → (P) and (R)
- (B) → (Q) and (S)
- (C) → (P) and (R)
- (D) → (P), (Q), (R), and (S)
Topper's Solved these Questions
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Long Answer Type
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
Similar Questions
Knowledge Check
Match the Column I and Column II.,B
 AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-q
AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-q
Match the two columns (Column-I & Column-II)
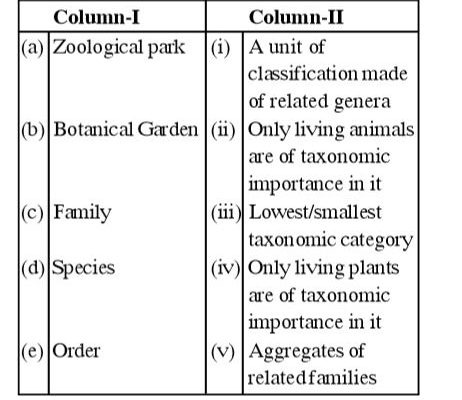
View SolutionMatch the entries in column I and column II with same dimensional formula

View SolutionMatch the entry in colum-I with the entry in column-II
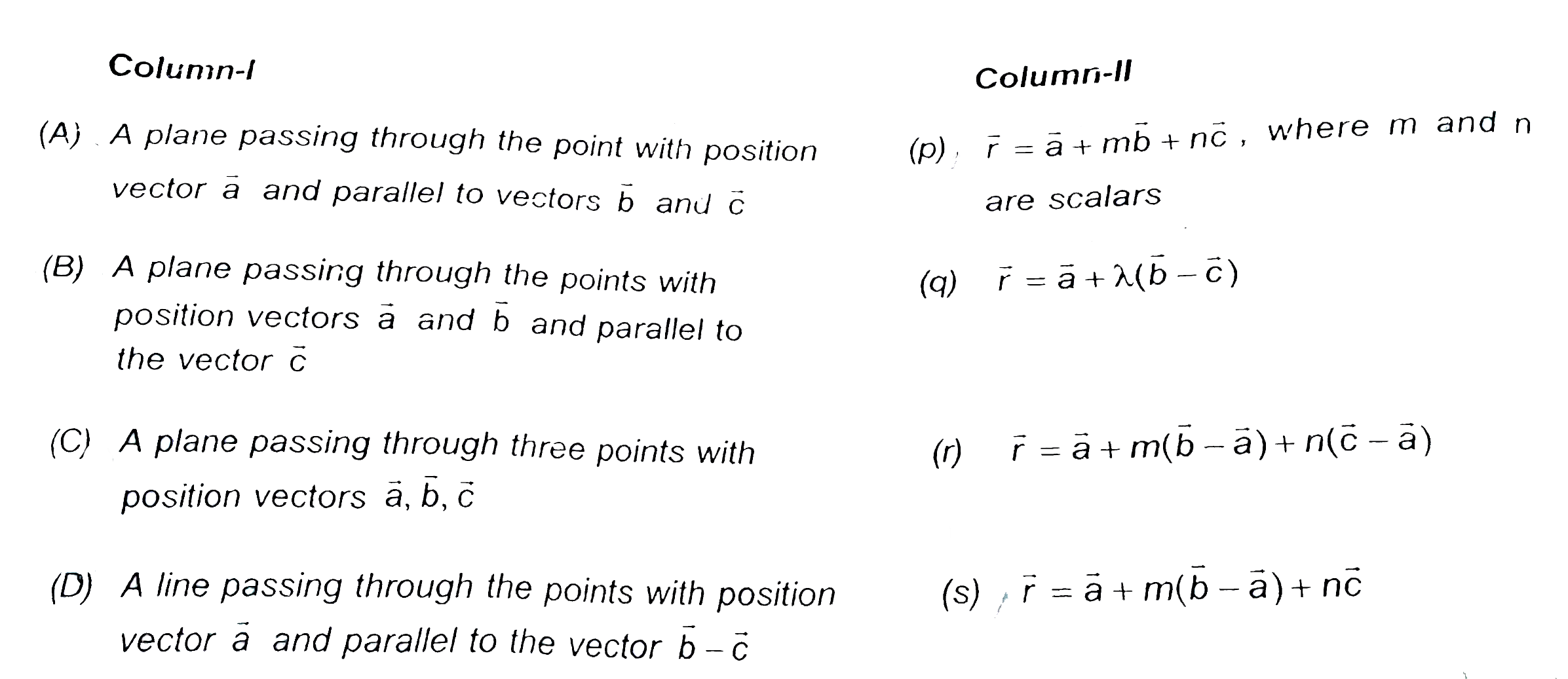
View SolutionMatch the entries in Column - I with those of Column - II and chosse the correct answer
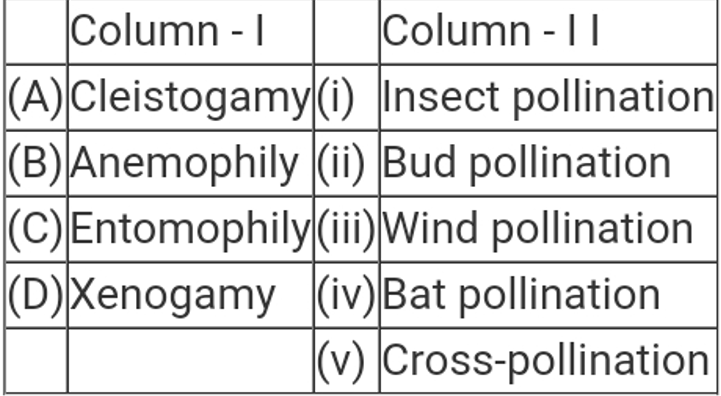
View SolutionMatch all the entries in column-I to all the entries in column-II

View SolutionMatch the entries in column II with the statements given in column I.

View SolutionThe correct match between the entries in column I and column II are :
View Solution


