A particle is prjected up an inclined with initial speed v=20m/s at an angle θ=30∘ with the plane. The component of its velocity perpendicular to the plane when it strikes the plane is:
The correct Answer is:5
Component of velocity perpendicular to the plane an landing = component of velocity perpendicular to the plane at the point of projection =20sin30∘=10m/s.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)19videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)19videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Long Answer Type5videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J10videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K10videos
MOVING CHARGES & MAGNETISM
Similar Questions
In the above problem, what is the component of its velocity perpendicular to the plane when it strikes at A ?
View SolutionA plane is inclined at an angle 30∘ with horizontal. The component of a vector →A=−10k perpendicular to this plane is: (here z-direction is vertically upwards)
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
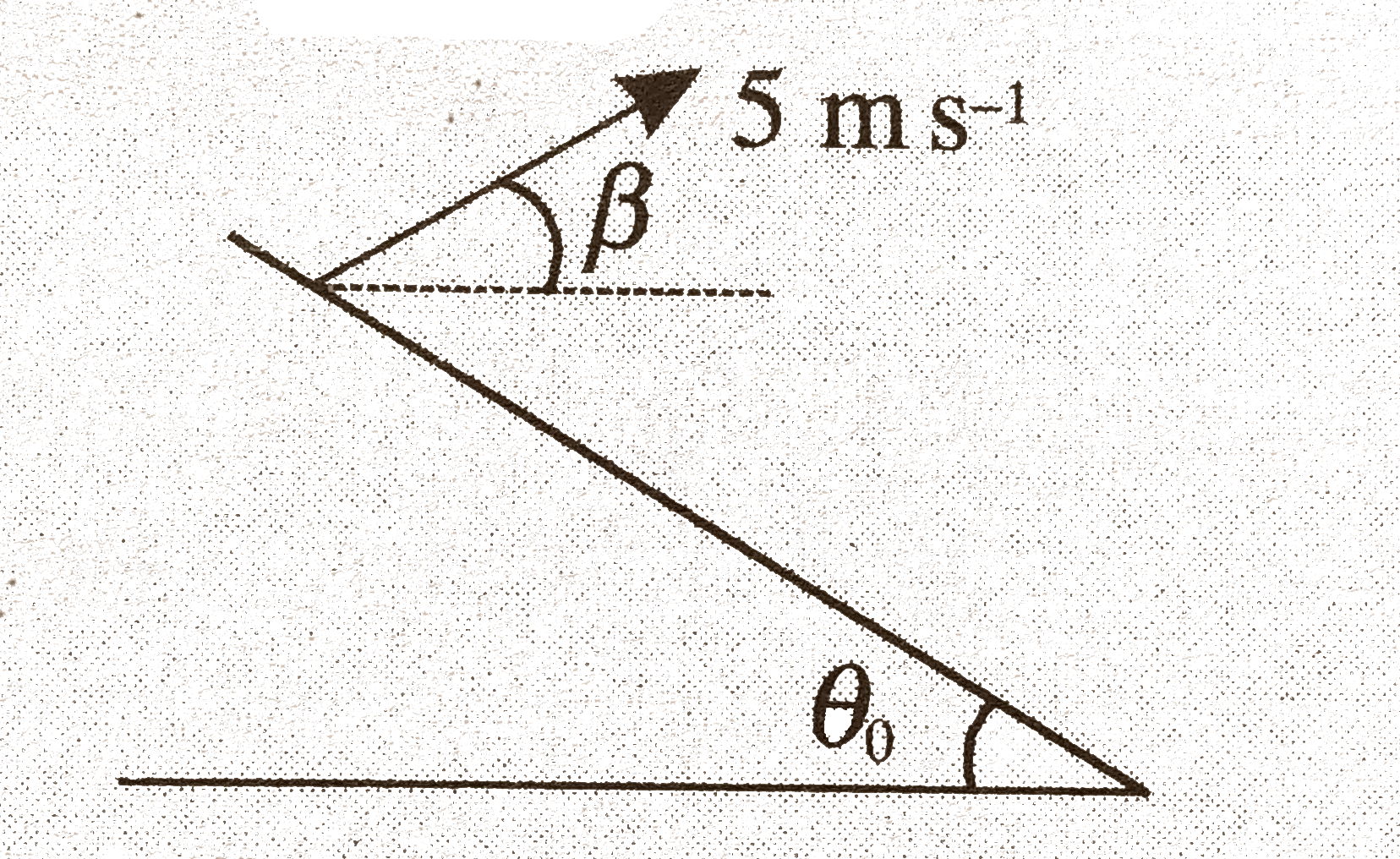 .View Solution
.View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
 View Solution
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
 View Solution
View Solution
A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclination 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h, the particle hits the block at some point on the inclined plane. Neglect friction at inclined.
Q. The value of height h isView SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .View Solution
.View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
 View Solution
View Solution

