A block of mass m is resting one a smooth horizontal surface. One end of a uniform rope of mass m/3 is fixed to the block, which is pulled in the horizontal direction by applying force F at the other end. The tension in the middle of the rope is
86F
17F
18F
78F
The correct Answer is:D
To find the tension in the middle of the rope when a block of mass m is pulled with a force F and the rope has a mass of m3, we can follow these steps:
Step 1: Determine the total mass of the system
The total mass of the system consists of the mass of the block and the mass of the rope. Therefore, the total mass M is given by:
M=m+m3=3m3+m3=4m3
Step 2: Calculate the acceleration of the system
Using Newton's second law, the net force F acting on the system is equal to the total mass times the acceleration a:
F=M⋅a
Substituting the total mass M:
F=4m3⋅a
Solving for acceleration a:
a=3F4m
Step 3: Analyze the left half of the rope
To find the tension at the middle of the rope, we can consider the left half of the rope and the block. The mass of the left half of the rope is m6 (since the total mass of the rope is m3, half of that is m6). The total mass being pulled by the tension TO at the middle point includes the mass of the block m and the mass of the left half of the rope m6:
Total mass on the left=m+m6=6m6+m6=7m6
Step 4: Apply Newton's second law to the left side
The tension TO at the middle of the rope is responsible for accelerating the total mass on the left side. Therefore, we can write:
TO=(7m6)⋅a
Substituting the expression for acceleration a:
TO=(7m6)⋅(3F4m)
Step 5: Simplify the expression for tension
Now, we can simplify the expression for TO:
TO=7m6⋅3F4m=7⋅3F6⋅4=21F24=7F8
Conclusion
Thus, the tension in the middle of the rope is:
TO=7F8
The total mass of the system consists of the mass of the block and the mass of the rope. Therefore, the total mass M is given by:
M=m+m3=3m3+m3=4m3
Using Newton's second law, the net force F acting on the system is equal to the total mass times the acceleration a:
F=M⋅a
Substituting the total mass M:
F=4m3⋅a
Solving for acceleration a:
a=3F4m
To find the tension at the middle of the rope, we can consider the left half of the rope and the block. The mass of the left half of the rope is m6 (since the total mass of the rope is m3, half of that is m6). The total mass being pulled by the tension TO at the middle point includes the mass of the block m and the mass of the left half of the rope m6:
Total mass on the left=m+m6=6m6+m6=7m6
The tension TO at the middle of the rope is responsible for accelerating the total mass on the left side. Therefore, we can write:
TO=(7m6)⋅a
Substituting the expression for acceleration a:
TO=(7m6)⋅(3F4m)
Now, we can simplify the expression for TO:
TO=7m6⋅3F4m=7⋅3F6⋅4=21F24=7F8
Thus, the tension in the middle of the rope is:
TO=7F8
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 249videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )16videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 0 (LONG ANSWER TYPE)4videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
A block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View SolutionA block of mass 10 kg lying on a smooth horizontal surface is being pulled by means of-a rope of mass 2 kg. If a force of 36N is applied at the end of the rope, the tension at the mid point of the rope is,
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
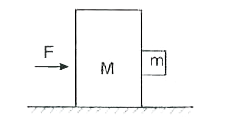 View Solution
View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is
 View Solution
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is
 View Solution
View SolutionA block of mass m as shown in figure is pulled by a force 40N. The tension at the middle of the block is
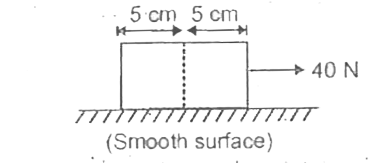 View Solution
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force F is applied at one end of rope. The force which the rope exerts on the block is:
View Solution

