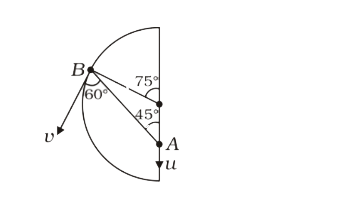
Two beads A and B move along a semicicular wir2 frame as shown in figure. The beads are connected by an inelastic string which always remain tight. At an instant the speed of A is u,∠BAC=45∘ and ∠BOC=75∘,where O is the centre of the semicicular arc. The speed of bead B at that instant is

√2u
u
u2√2
√23u
The correct Answer is:A
Distance AB - constant
∴ Component of v along
BA = component of u along BA
or vcos6∘=ucos45∘
or v=√2u
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )16videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I29videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 175videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
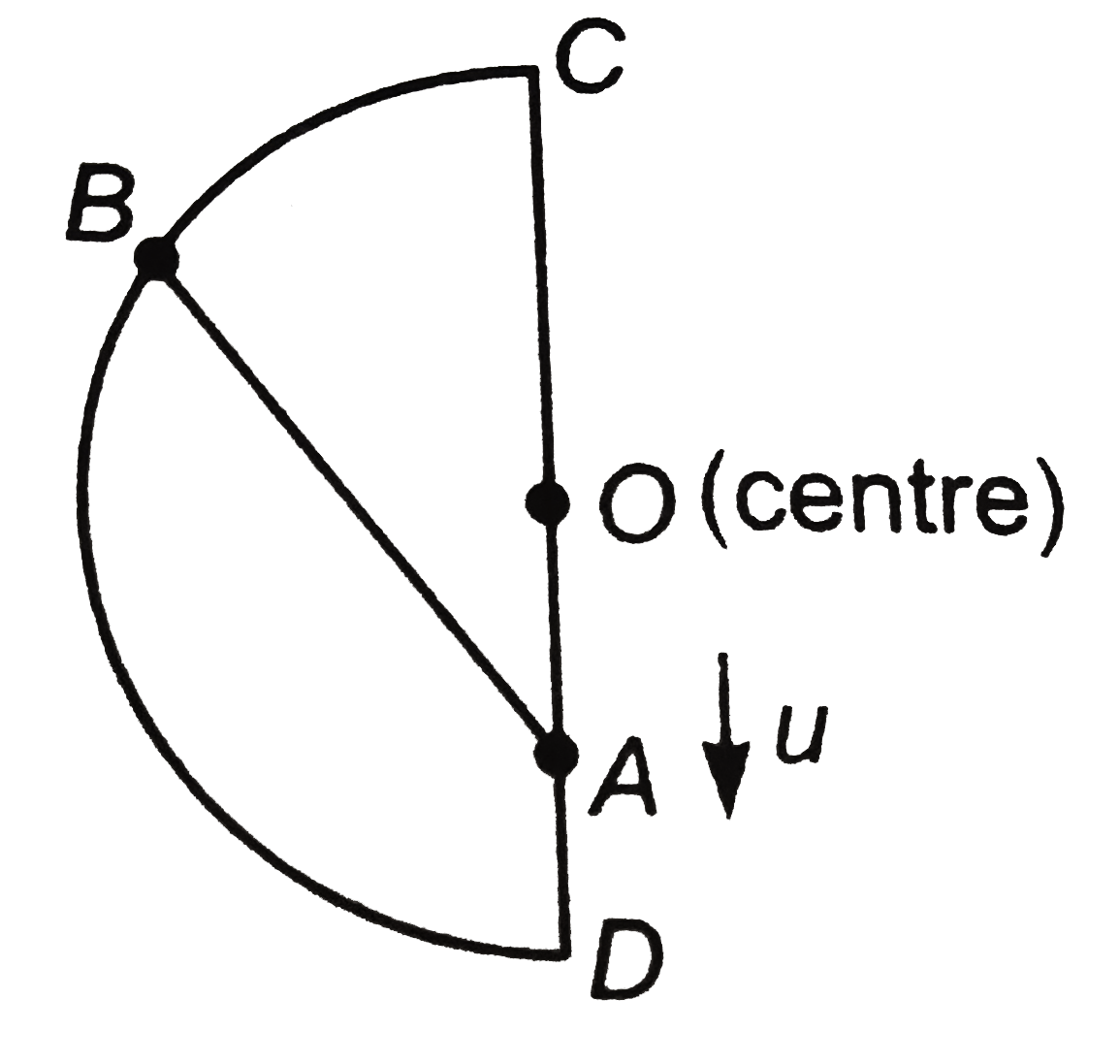
Two beads A and B move along a semicircular wire frame as shown in figure. The beads are connected by an inelastic string which always remains tight . At an instant the speed of A is u,∠BAC=45∘andBOC=75∘,where O is the centre of the semicircular arc. The speed of bead B at that instant is
 View Solution
View SolutionTwo block A and Bmove along a semicircular wire frame as shown in figure. The beads are connected by an inelastic string wich always remains tight . At an instant the speed of A is u,∠BAC=45∘andBOC=75∘,where O is the center of the semicircular are. The speed of bead B at that instant is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two particles A and B intiallly at rest, move towards each other under a mutual force of attraction. AT the instant when the speed of A is v and the speed of B is 2 v, the speed of the centre of mass of the system is
AzeroBvC1.5 vD3 v - Question 2 - Select One
Two particles A and B, initially at rest, moves towards each other under a mutual force of attraction. At the instant when the speed of A is v and the speed of B is 2 v, the speed of centre of mass is
AzeroBvC1.5 vD3 v
A rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
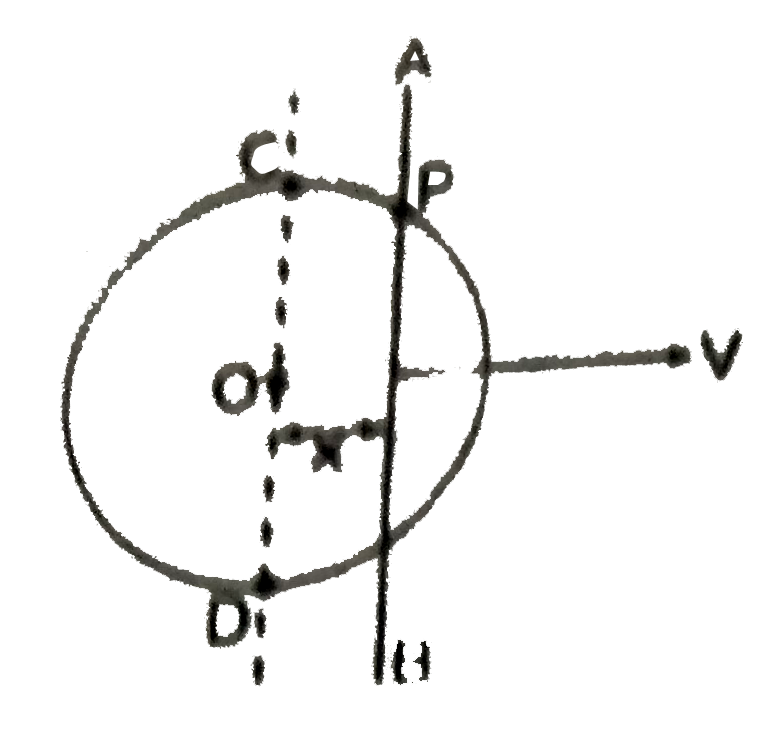
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.View Solution
A rod AB is moving on a fixed circle of radius R with constant velocity v as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distancex=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.View SolutionTwo beads of masses m1 and m2 are connected to each other by massless string. Both beads are free to mover over fixed smooth circular loop in vertical plane. At any instant they are in the position shown and subtends angle 90∘ at centre. Find tangential accelerations of both beads and tension in the string if string remains taut.
 View Solution
View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
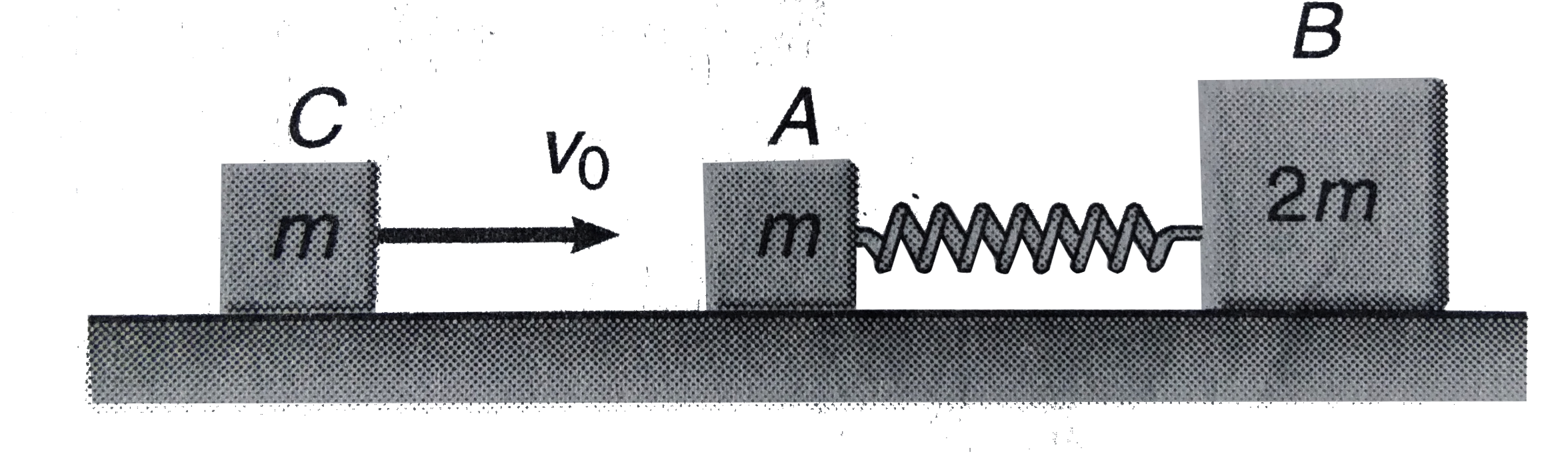 View Solution
View SolutionA bead B of mass 'm' can travel without frictionn on a smooth horizontalwire xx′. The bead is connected to a block of identical mass by an ideal string passing over an ideal pulley. The system, as shown, is in vertical plane.

The system is allowed to fall. Find the speed of block A at the instant when string connected to the bead B makes an angle 37∘ with vertical.View SolutionA fixed U-shaped smooth wire has a semi-circular bending between A and B as shown in the figure. A bead of mass 'm' moving with uniform speed v through the wire enters the semicircular bend at A and leaves at B. The magnitude of average force exerted by the bead on the part AB of the wire is
 View Solution
View Solution

