A block A of mass 4 kg is placed on another block B of mass 5 kg , and the block B rests on a smooth horizontal table . For sliding block A on B , a horizontal force of 12 N is required to be applied on A How much maximum force can be applied on B so that both A and B move togrther ? Also find out acceleration produced by this force .
(a)15 N
(b)25 N
(c)27 N
(d)48 N
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the blocks and apply Newton's laws of motion.
Step 1: Identify the masses and forces
- Mass of block A (m1) = 4 kg
- Mass of block B (m2) = 5 kg
- Force required to slide block A on B (F) = 12 N
Step 2: Determine the maximum static friction force
The maximum static friction force (f_max) that can act between blocks A and B is what allows them to move together without slipping. This can be calculated using the formula:
fmax=μs⋅N
where N is the normal force acting on block A due to its weight. Since block A is resting on block B, the normal force is equal to the weight of block A:
N=m1⋅g=4kg⋅9.8m/s2=39.2N
Step 3: Calculate the maximum static friction force
Assuming the coefficient of static friction (μs) is sufficient to prevent slipping, we can set:
fmax=12N
This means that the maximum force that can be applied on block B without causing A to slip off is equal to the maximum static friction force.
Step 4: Calculate the total mass when both blocks move together
When both blocks move together, the total mass M is:
M=m1+m2=4kg+5kg=9kg
Step 5: Calculate the maximum force that can be applied on block B
The maximum force FB that can be applied on block B, so that both A and B move together, is equal to the maximum static friction force:
FB=fmax=12N
Step 6: Calculate the acceleration produced by this force
Using Newton's second law, the acceleration a of the system when the force FB is applied is given by:
FB=M⋅a
Rearranging gives:
a=FBM=12N9kg≈1.33m/s2
Final Answers
- The maximum force that can be applied on block B so that both A and B move together is 12 N.
- The acceleration produced by this force is approximately 1.33 m/s².
- Mass of block A (m1) = 4 kg
- Mass of block B (m2) = 5 kg
- Force required to slide block A on B (F) = 12 N
The maximum static friction force (f_max) that can act between blocks A and B is what allows them to move together without slipping. This can be calculated using the formula:
fmax=μs⋅N
where N is the normal force acting on block A due to its weight. Since block A is resting on block B, the normal force is equal to the weight of block A:
N=m1⋅g=4kg⋅9.8m/s2=39.2N
Assuming the coefficient of static friction (μs) is sufficient to prevent slipping, we can set:
fmax=12N
This means that the maximum force that can be applied on block B without causing A to slip off is equal to the maximum static friction force.
When both blocks move together, the total mass M is:
M=m1+m2=4kg+5kg=9kg
The maximum force FB that can be applied on block B, so that both A and B move together, is equal to the maximum static friction force:
FB=fmax=12N
Using Newton's second law, the acceleration a of the system when the force FB is applied is given by:
FB=M⋅a
Rearranging gives:
a=FBM=12N9kg≈1.33m/s2
- The maximum force that can be applied on block B so that both A and B move together is 12 N.
- The acceleration produced by this force is approximately 1.33 m/s².
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
16 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
12N of force required to be applied on A to slip on B. Find the maximum horizontal force F to be applied on B so that A and B moves together.

View SolutionA 4 kg block A is placed on the top of 8 kg block B which rests on a smooth table.

A just slips on B when a force of 12 N is applied on A. Then the maximum horizontal force F applied on B to make both A and B move together, is
View Solution
Knowledge Check
A block A of mass 4 kg is placed on another block B of mass 5 kg and the block rests on a smooth horizontal table. For sliding the block A on B, a horizontal force of 12 N is required to be applied on it. The maximum horizontal force that can be applied on B so that both A and B move together and the acceleration produced by this force is
 A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
A block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View SolutionA small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A. A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time elapsed before the block B separates from A.
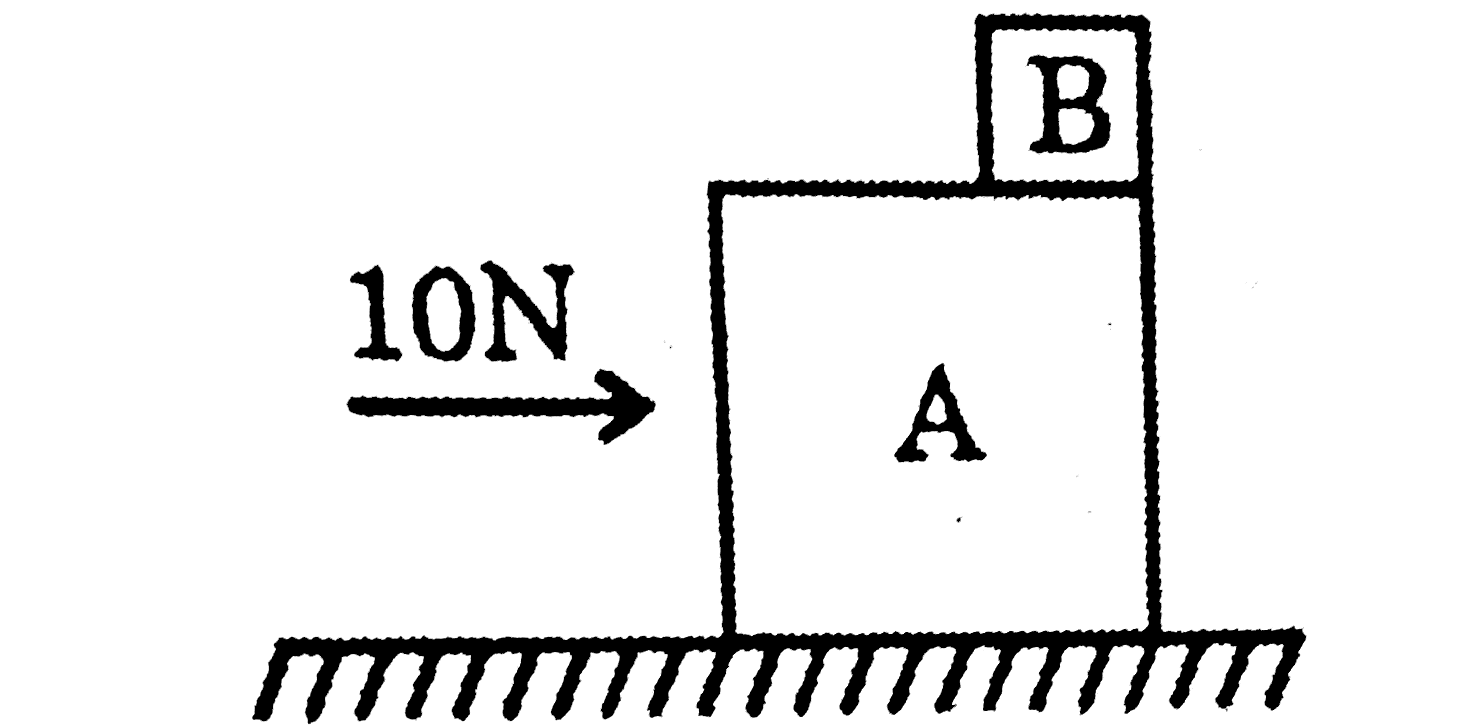
View SolutionTwo block A and B of masses 5 kg. and 3 kg. respectively rest on smooth horizontal surface with B over A. The coefficient of friction between A and B. 0.5 the maximum horizontal force that can be applied to A so that there will be motion of A and B without separation is :-
View SolutionBlock A of mass 1kg is placed on the rough surface of block B of mass 3kg. Block B is placed on smooth horizontal surface. Blocks are given the velocities as shown. Find net work done by the frictional force. [in (−)veJ].
 .
.
View SolutionThree blocks of masses 3kg,2kg and 1kg are placed side by side on a smooth surface as shown in figure. A horizontal force of 12N is applied on 3kg block. Find the net force on 2kg block.

View SolutionThree blocks of masses 3kg,2kg and 1kg are placed side by side on a smooth surface as shown in figure. A horizontal force of 12N is applied on 3kg block. Find the net force on 2kg block.

View Solution
