Two block A and B of masses 5 kg. and 3 kg. respectively rest on smooth horizontal surface with B over A. The coefficient of friction between A and B. 0.5 the maximum horizontal force that can be applied to A so that there will be motion of A and B without separation is :-
1.5
2.5
40
5
To solve the problem, we need to determine the maximum horizontal force that can be applied to block A so that both blocks A and B move together without separation. Here’s a step-by-step solution:
Step 1: Identify the masses and coefficients
- Mass of block A (m_A) = 5 kg
- Mass of block B (m_B) = 3 kg
- Coefficient of friction (μ) between A and B = 0.5
Step 2: Calculate the total mass of the system
The total mass (M) of the system (blocks A and B) is:
M=mA+mB=5kg+3kg=8kg
Step 3: Define the applied force and acceleration
Let the applied horizontal force on block A be F. Since both blocks must move together without separation, they will have the same acceleration (a). The relationship between the applied force and the acceleration of the system can be expressed as:
F=M⋅a=8a
Step 4: Analyze the forces acting on block B
For block B to not slip off block A, the frictional force must be sufficient to provide the necessary acceleration. The maximum static friction force (f_max) that can act on block B is given by:
fmax=μ⋅N
where N is the normal force acting on block B. The normal force (N) is equal to the weight of block B:
N=mB⋅g=3kg⋅9.8m/s2=29.4N
Thus, the maximum static friction force is:
fmax=0.5⋅29.4N=14.7N
Step 5: Set up the equation for maximum friction
The frictional force must equal the force required to accelerate block B:
fmax=mB⋅a
Substituting the values, we have:
14.7N=3kg⋅a
From this, we can solve for acceleration (a):
a=14.7N3kg=4.9m/s2
Step 6: Substitute acceleration back into the force equation
Now, substitute the value of acceleration back into the equation for the applied force:
F=8a=8⋅4.9m/s2=39.2N
Step 7: Conclusion
The maximum horizontal force that can be applied to block A so that there will be motion of A and B without separation is approximately:
F≈39.2N
Final Answer
The maximum horizontal force that can be applied to A without separation is 39.2 N.
---
- Mass of block A (m_A) = 5 kg
- Mass of block B (m_B) = 3 kg
- Coefficient of friction (μ) between A and B = 0.5
The total mass (M) of the system (blocks A and B) is:
M=mA+mB=5kg+3kg=8kg
Let the applied horizontal force on block A be F. Since both blocks must move together without separation, they will have the same acceleration (a). The relationship between the applied force and the acceleration of the system can be expressed as:
F=M⋅a=8a
For block B to not slip off block A, the frictional force must be sufficient to provide the necessary acceleration. The maximum static friction force (f_max) that can act on block B is given by:
fmax=μ⋅N
where N is the normal force acting on block B. The normal force (N) is equal to the weight of block B:
N=mB⋅g=3kg⋅9.8m/s2=29.4N
fmax=0.5⋅29.4N=14.7N
The frictional force must equal the force required to accelerate block B:
fmax=mB⋅a
Substituting the values, we have:
14.7N=3kg⋅a
From this, we can solve for acceleration (a):
a=14.7N3kg=4.9m/s2
Now, substitute the value of acceleration back into the equation for the applied force:
F=8a=8⋅4.9m/s2=39.2N
The maximum horizontal force that can be applied to block A so that there will be motion of A and B without separation is approximately:
F≈39.2N
The maximum horizontal force that can be applied to A without separation is 39.2 N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Two block A and B of masses 6kg and 3kg rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is 0.4 the maximum horizontal force which can make them move without separation is

View SolutionTwo block A and B of masses 6kg and 3kg rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is 0.4 the maximum horizontal force which can make them move without separation is

View Solution
Knowledge Check
A block A of mass 4 kg is placed on another block B of mass 5 kg and the block rests on a smooth horizontal table. For sliding the block A on B, a horizontal force of 12 N is required to be applied on it. The maximum horizontal force that can be applied on B so that both A and B move together and the acceleration produced by this force is
 A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.Two blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
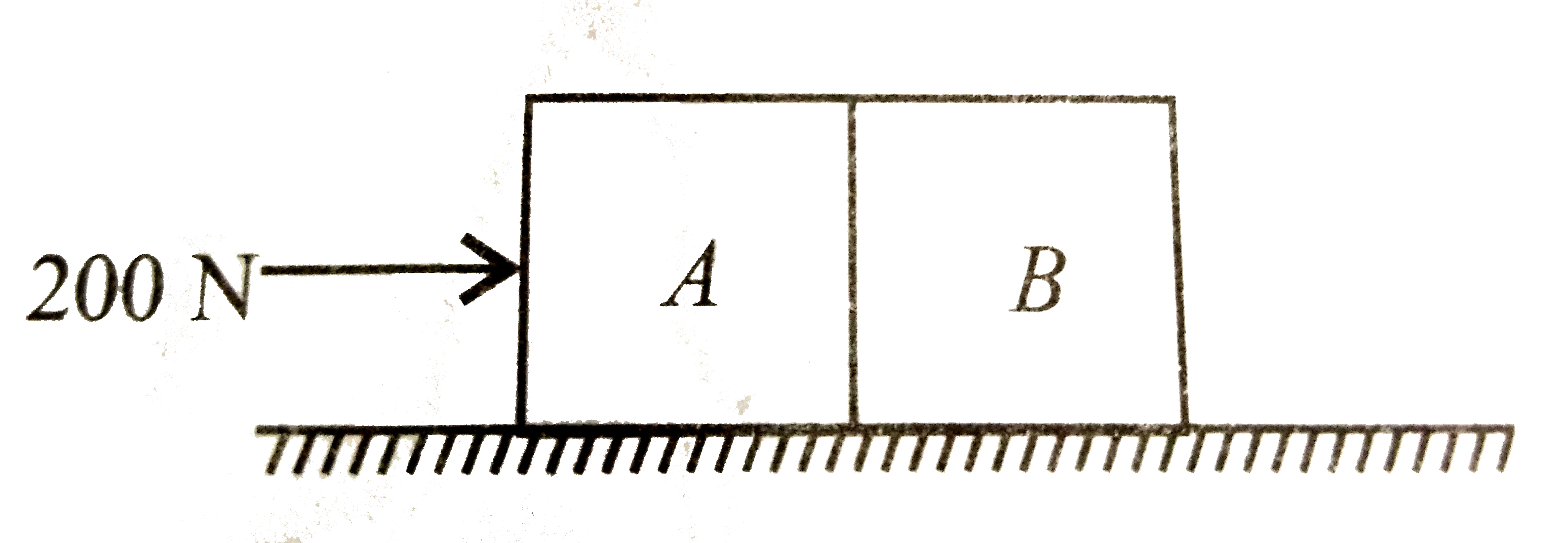 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
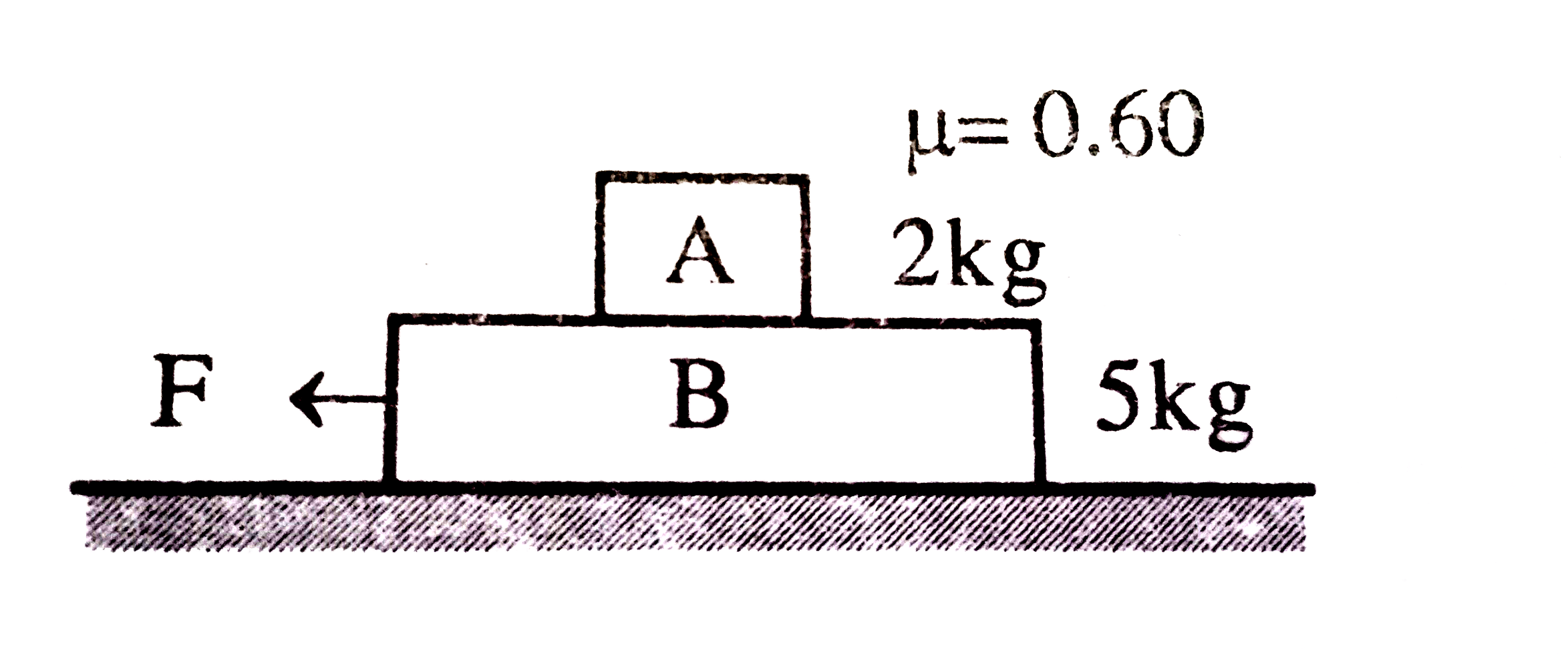
Two block (A) 2kg and (B) 5kg rest one over the other on a smooth horizontal plane. The cofficient of static and dynamic friction between (A) and (B) is the sae and equal to 0.60. The maximum horizontal force that can be applied to (B) in order that both (A) and (B) do not have any relative motion:
View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

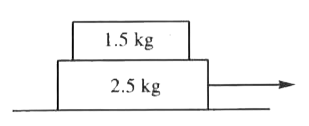
View SolutionOn a smooth table two blocks of masses 2.5kg and 1.5kg are placed one over the other as shown in figure. If the coefficient of static friction between two blocks is 0.2, the maximum horizontal force to be applied on the lower block so that the two blocks move together is (g = ms−2)
View SolutionMeasles of A and B 10 kg and 5 kg respectively.y A is on smooth surface coefficient of friction between A and B is 0.4 if F=75N friction between the block is __ N.

View SolutionTwo blocks A and B of masses 2kg and 3kg respectively, are placed on a horizontal surface as shown (one on top of other). Find the ratio of magnitude of normal reaction between A and B to that between B and the surface, respectively

View SolutionA block A of mass m kg lies on a block B of mass m kg. B in turn lies on smooth horizontal plane. The coefficient of friction between A and B is μ. Both the blocks are initially at rest. A horizontal force F is applied to lower block B at t = 0 till the lower block B undergoes a displacement of magnitude L. Match the statements in Table-1 with the results in Table-2.

View Solution
