A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A plumb bob is suspended from the roof of the car by a light rigid rod. The angle made by the rod with the vertical is
zero
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the plumb bob suspended from the roof of the car that is moving in a circular path. Here are the steps to find the angle made by the rod with the vertical:
Step 1: Identify the forces acting on the plumb bob
The two main forces acting on the plumb bob are:
1. The gravitational force (weight) acting downwards, Fg=mg
2. The centripetal force required to keep the car moving in a circular path, which causes the bob to deflect from the vertical.
Step 2: Calculate the centripetal acceleration
The centripetal acceleration ac can be calculated using the formula:
ac=v2r
Where:
- v=10m/s (the speed of the car)
- r=10m (the radius of the circular track)
Substituting the values:
ac=(10m/s)210m=100m2/s210m=10m/s2
Step 3: Relate the forces to find the angle
The angle θ made by the rod with the vertical can be found using the tangent function:
tanθ=oppositeadjacent=acg
Where:
- ac=10m/s2 (centripetal acceleration)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
tanθ=10m/s210m/s2=1
Step 4: Calculate the angle θ
To find θ, we take the arctangent:
θ=tan−1(1)=45∘
Conclusion
The angle made by the rod with the vertical is 45∘.
The two main forces acting on the plumb bob are:
1. The gravitational force (weight) acting downwards, Fg=mg
2. The centripetal force required to keep the car moving in a circular path, which causes the bob to deflect from the vertical.
The centripetal acceleration ac can be calculated using the formula:
ac=v2r
Where:
- v=10m/s (the speed of the car)
- r=10m (the radius of the circular track)
ac=(10m/s)210m=100m2/s210m=10m/s2
The angle θ made by the rod with the vertical can be found using the tangent function:
tanθ=oppositeadjacent=acg
Where:
- ac=10m/s2 (centripetal acceleration)
- g=10m/s2 (acceleration due to gravity)
tanθ=10m/s210m/s2=1
To find θ, we take the arctangent:
θ=tan−1(1)=45∘
The angle made by the rod with the vertical is 45∘.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I29videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
A car is moving along a circular track of radius 10√3m with a constant speed of 36kmph. A plumb bob is suspended from the roof of the car by a light rigid rod of length Im. The angle made by the rod with the track is (g=10ms−2 )
View SolutionA car of mass 300 kg is travelling on a circular track of radius 100 m with a constant speed of 60 m/s
Calculate the angular momentum ?View SolutionA car of mass 300 kg is travelling on a circular track of radius 100 m with a constant speed of 60 m/s
Calculate the angular momentum ?View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionTension in the rope at the rigid support is (g=10m/s2)
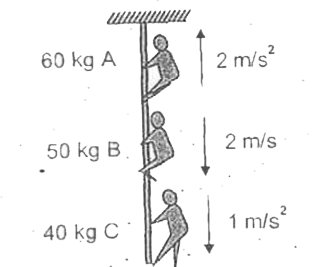 View Solution
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionA car of mass 1000 kg moves on a circular track of radius 100 m with a speed of 40 m/s. Calculate the magnitude of its angular momentum relative to the centre of the track.
View SolutionA car of maas M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
View SolutionFigure shows as rod of length 20 cm pivoted near an end and which is made to rotate in a horizontal plane with a constant angular speed. A ball ofmass m is spuspended by a string angular also of length 20 cm from the other end of the rod. If the angle θ made by the stirng with the vertical is 300. find the anglular speed of the rotation. Take g=10ms2
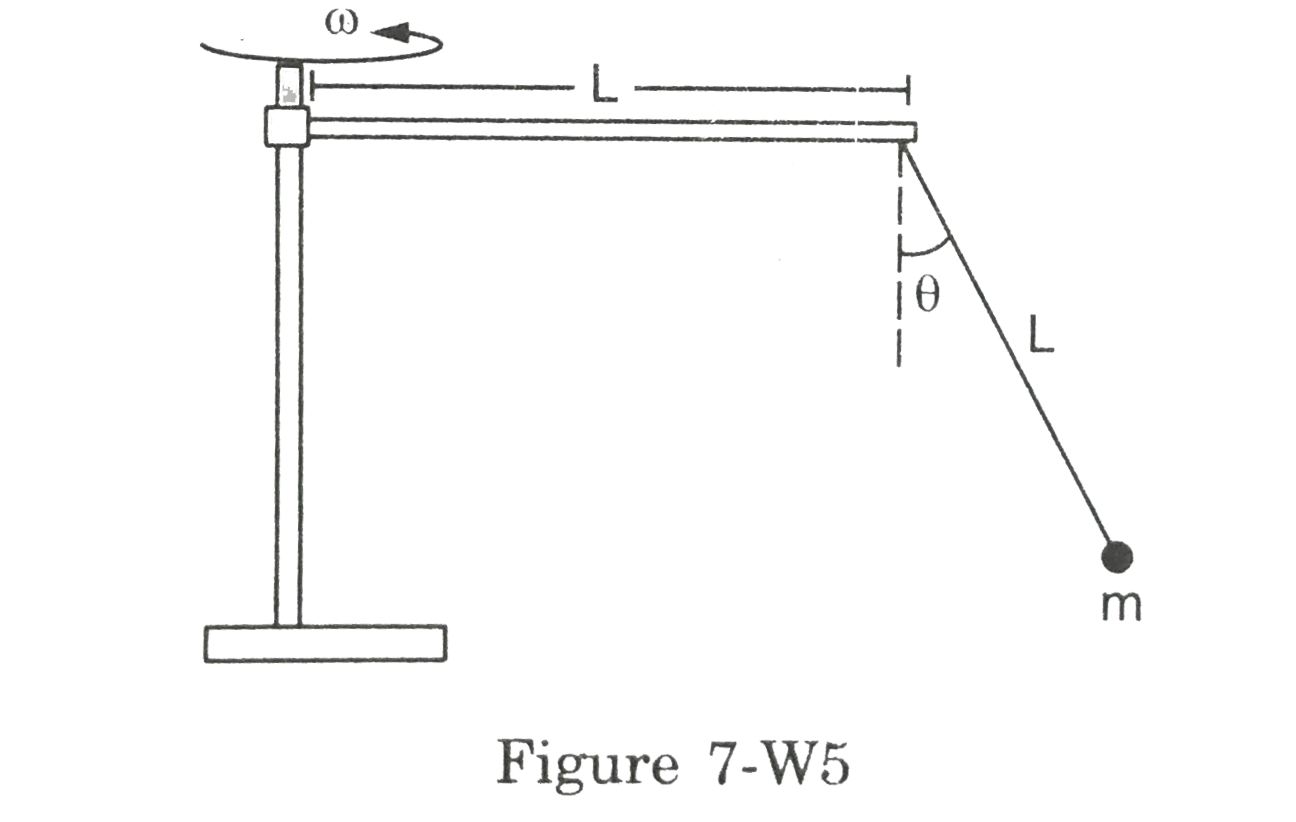 View Solution
View SolutionA car is moving on a horizontal circular road of radius 0.1 km with constant speed. If coefficient of friction between tyres of car and road is 0.4, then speed of car may be (g=10m/s2)
View Solution

