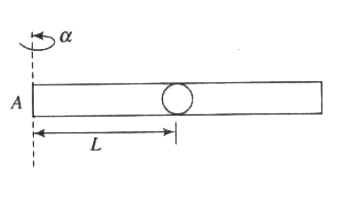
A long horizontal rod has a bead which can slide along its length and initially placed at a 
distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is
√μ/α
μ/√α
1√μα
Infinitesimal
The correct Answer is:A
When we are giving angular acceleration to the rod, the bead is also having a tangential acceleration at=Lα . This will happen when a force is exerted on the bead by the rod. The bead has a tendency to move away from the centre. But due to the friction between the bead and the rod, this does not happen to the extent to which frictional force is capable of holding the bead. The frictional force here provides the necessary centripetal force. If instantaneous angular velocity is ω then mLω2=μ(ma)
mLω2=μmLα⇒ω2=μα . by applying ω=ω0+αt we get ω=αt
a2t2=μα⇒t=√μα
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I29videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
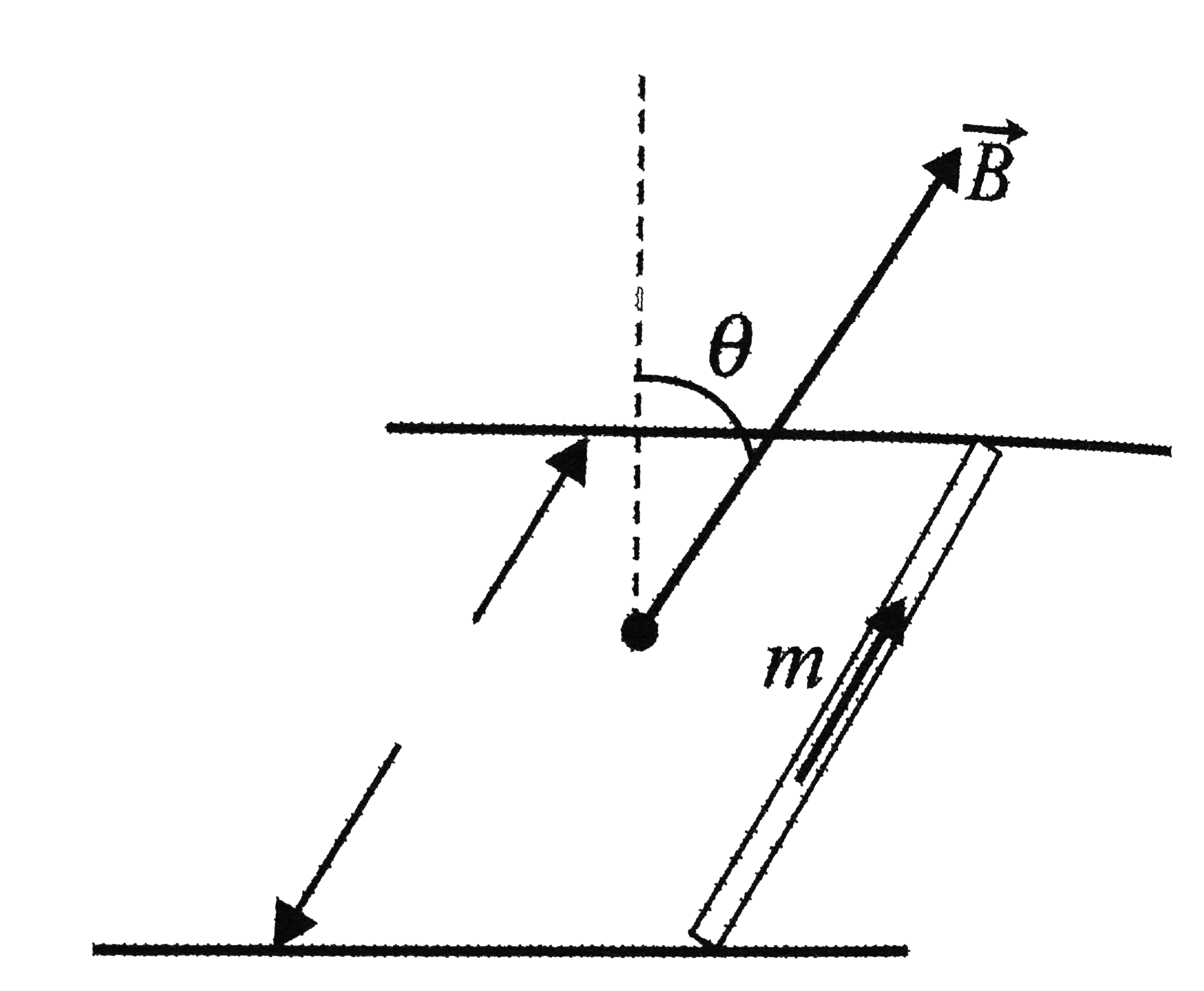 View Solution
View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration
A. the normal reaction on the bead will be constant h magnitude and direction both
B. the magnitude of the normal reaction on the bead will be variable
C. the magnitude of friction force on the bead will be constant
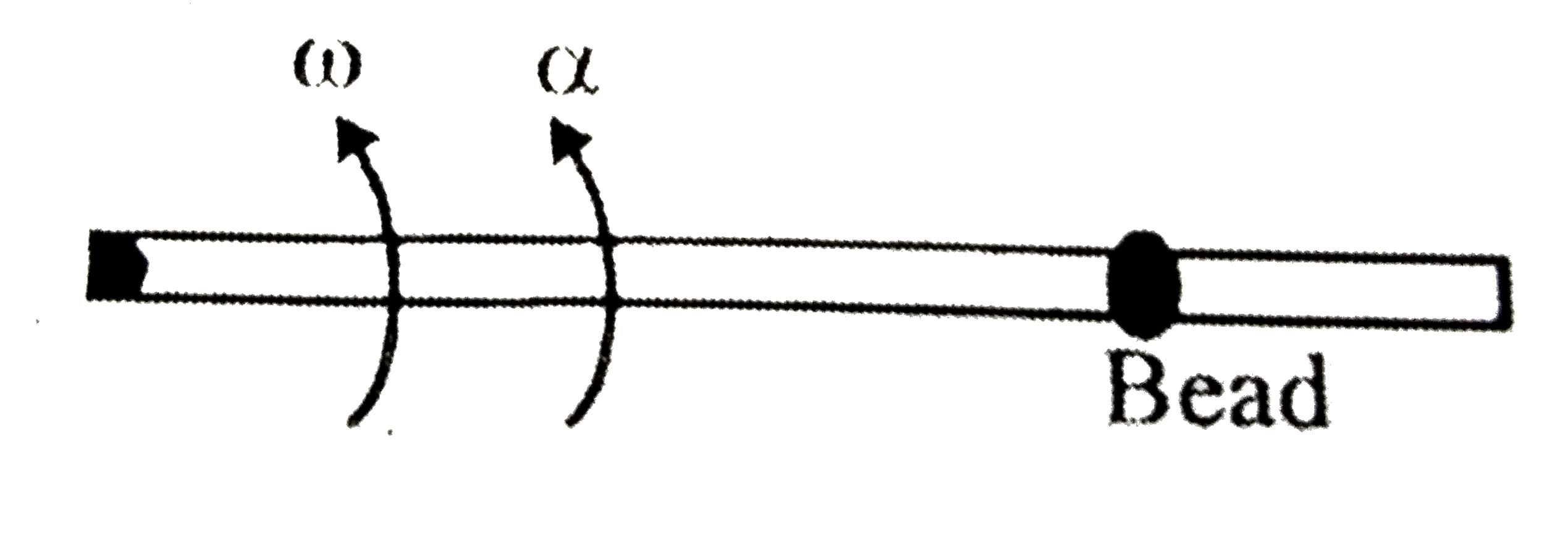
D. the magnitude of friction force on the bead will be variableView SolutionA bead is contrained to move on rod in granvity free space as shown in figure. The rod rotating with ,angular velocity and angulnr acceleration α about its end. If μ is coefficient of friction. Mark the correct option. ( Rod rotates in the plane of paper.)
 View Solution
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
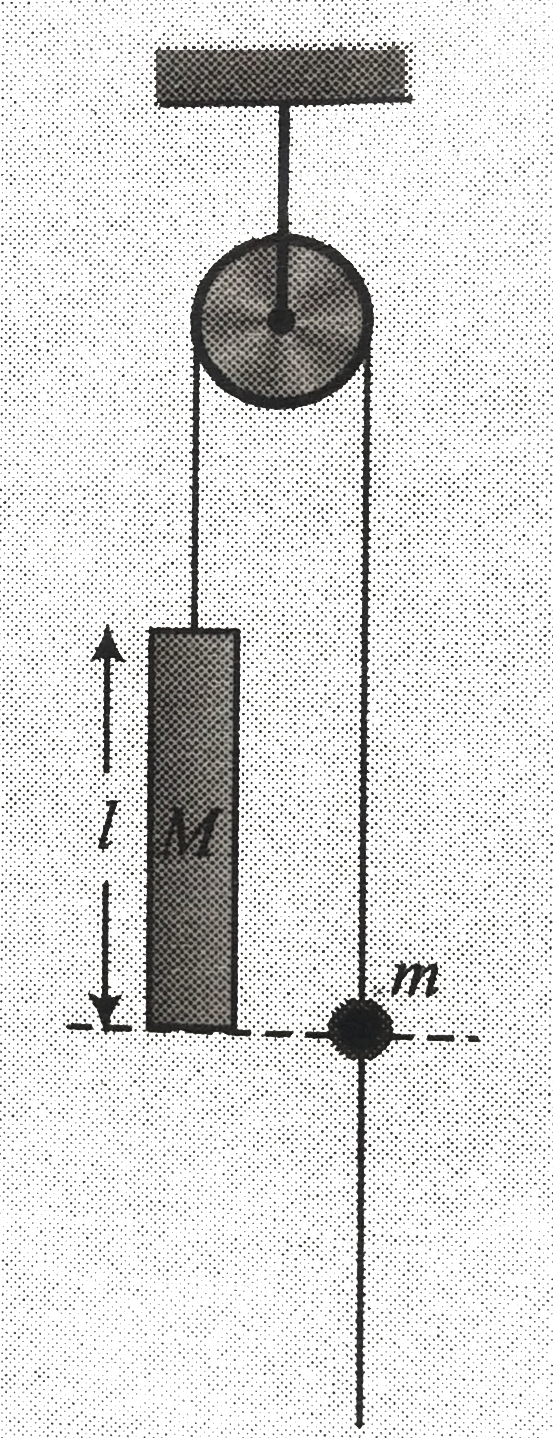 View Solution
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
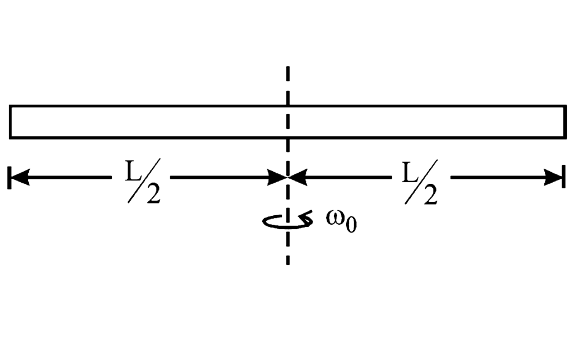 View Solution
View SolutionA thin rod of length 1m is fixed in a vertical position inside a train, which is moving horizontally with constant acceleration 4ms−2.A bead can slide on the rod and friction coefficient between them is 0.5. If the bead is released from rest at the top of the rod , it will reach the bottom in
View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :
 View Solution
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
 View Solution
View SolutionA non-conducting rod AB of length l has total charge Q . The rod is rotated about an axis passing through a point (l/3) distance from one end and perpendicular to plane of rod with constant angular speed omega, the magnetic moment of rod is
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 View Solution
View Solution

