A plate moves normally with the speed v1 towads a horizontal jet of uniform area of cross-section. The jet discharge water at the rate of volume V per second at a speed of v2. The density of water is ρ. Assume that water splashes along the surface of the plate ar right angles to the original motion. The magnitude of the force action on the plate due to the jet of water is
(a)ρVv1
(b)ρV(v1+v2)
(c)ρVv1+v2V21
(d)ρ[Vv2](v1+v2)2
The correct Answer is:D
To solve the problem, we need to determine the magnitude of the force acting on a plate due to a horizontal jet of water. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have a plate moving towards a horizontal jet of water. The plate moves with a speed v1 and the jet discharges water at a rate of volume V per second with a speed v2. The density of water is ρ.
Hint: Visualize the scenario and draw a diagram to understand the directions of the velocities.
Step 2: Determine the Change in Momentum
The force acting on the plate due to the jet of water can be calculated using the principle of momentum change. The change in momentum per unit time (force) is given by:
F=ΔPΔt
where ΔP is the change in momentum.
Hint: Remember that momentum P is defined as mass times velocity.
Step 3: Relate Momentum to Mass and Velocity
The momentum P can be expressed as:
P=m⋅v
where m is mass and v is velocity. The change in momentum when the water hits the plate can be expressed as:
ΔP=mass×Δv
where Δv is the change in velocity of the water as it strikes the plate.
Hint: Consider how the water's velocity changes when it strikes the plate.
Step 4: Calculate the Change in Velocity
Since the water is moving towards the plate with speed v2 and the plate is moving towards the water with speed v1, the effective change in velocity Δv when the water hits the plate is:
Δv=v1+v2
Hint: Think about the direction of the velocities and how they combine.
Step 5: Find the Mass Flow Rate
The mass flow rate of the water can be expressed as:
mass flow rate=ρ⋅V
where V is the volume of water discharged per second.
Hint: Use the definition of density to relate mass and volume.
Step 6: Substitute into the Force Equation
Now, substituting the mass flow rate into the force equation, we have:
F=mass flow rate×Δv=ρV(v1+v2)
Hint: Ensure that you are using the correct units for each variable.
Step 7: Finalize the Expression for Force
Thus, the magnitude of the force acting on the plate due to the jet of water is:
F=ρV(v1+v2)
Hint: Check if this expression matches any of the provided options in the question.
Conclusion
The final expression gives us the force acting on the plate due to the water jet. If the options are provided, we can identify the correct one based on our derived formula.
We have a plate moving towards a horizontal jet of water. The plate moves with a speed v1 and the jet discharges water at a rate of volume V per second with a speed v2. The density of water is ρ.
The force acting on the plate due to the jet of water can be calculated using the principle of momentum change. The change in momentum per unit time (force) is given by:
The momentum P can be expressed as:
Since the water is moving towards the plate with speed v2 and the plate is moving towards the water with speed v1, the effective change in velocity Δv when the water hits the plate is:
The mass flow rate of the water can be expressed as:
Now, substituting the mass flow rate into the force equation, we have:
Thus, the magnitude of the force acting on the plate due to the jet of water is:
The final expression gives us the force acting on the plate due to the water jet. If the options are provided, we can identify the correct one based on our derived formula.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I29videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
A flat plate moves normally towards a discharging jet of water at the rate of 3m/s. The jet discharges the water at the rate of 0.1m3/s and at the speed of 18m/s. The force exerted on the plate due to the jet is
View SolutionThe horizontal speed of a jet of water is 100 cm/sec and 50cm3 of water hits the plate each second. Assume that the water moves parallel to the plate after striking it. The force exerted on the stationary plate if it is held perpendicular to the jet of water is :
View SolutionThe fire fighters attach brass jets at the end of water pipes. Why?
View SolutionA horizontal jet of water coming out of a pipe of area of cross - section 20 cm2 hits a vertical wall with a velocity of 10 ms−1 and rebounds with the same speed. The force exerted by water on the wall is,
View SolutionWater flows steadily through a horizontal pipe of a variable cross-section. If the pressure of the water is p at a point , where the speed of the flow is v. What is the pressure at another point , where the speed of the flow is 2 v ? Let the density of water be 1gcm−3.
View SolutionWhich one emits jet of water when disturbed
View SolutionPerforated surface plate of water vascular system is
View Solution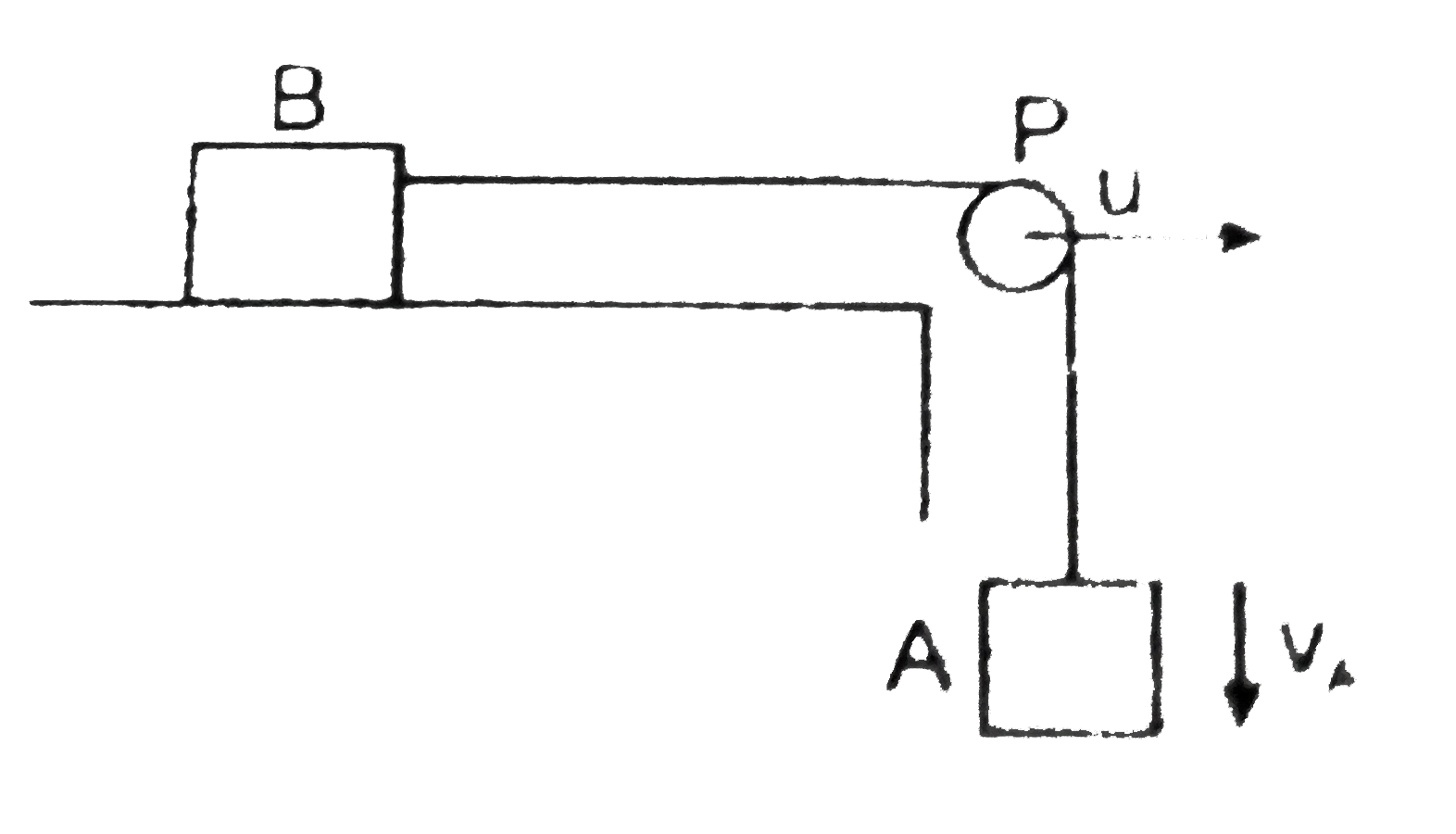
In the figure the pulley P moves to the right with a constant speed u. The downward speed of A is vA and the speed of B to the right VB.View SolutionA parallel plate capacitors of plate area A has a total surface charge density +σ on one plate and a total surface charge density −σ on the other plate. The force one plate due to the other plate is given by :
View SolutionIn a certain gravity free space, the piston of an injection is being pushed so that the water jet comes out with a speed v. The area of the piston is much greater than the orifice of the injection.
View Solution

