A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
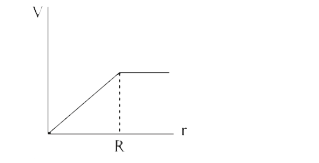
The correct Answer is:C
To solve the problem of determining the speed v of a test mass undergoing circular motion in a spherically symmetric gravitational system, we will analyze two cases based on the distance r from the center of the system.
Step 1: Define the mass density and gravitational field
Given the mass density:
ρ={ρ0for r<R0for r≥R
The gravitational field g at a distance r from the center can be derived using Gauss's law for gravity.
Step 2: Case 1: For r≥R
When r≥R, the gravitational field g is due to the entire mass enclosed within radius R. The mass M within radius R can be calculated as:
M=ρ0⋅43πR3
The gravitational field g at distance r (where r≥R) is given by:
g=GMr2=G(ρ0⋅43πR3)r2
Step 3: Relate gravitational force to centripetal force
For circular motion, the centripetal force required is provided by the gravitational force:
mv2r=mg
Substituting for g:
mv2r=m⋅G(ρ0⋅43πR3)r2
Cancelling m from both sides:
v2r=G(ρ0⋅43πR3)r2
Rearranging gives:
v2=G(ρ0⋅43πR3)r
Thus, we find:
v∝1√r
Step 4: Case 2: For r<R
For r<R, the gravitational field g is due only to the mass within radius r:
M′=ρ0⋅43πr3
Thus, the gravitational field g is:
g=GM′r2=G(ρ0⋅43πr3)r2=Gρ0⋅43πr3
Step 5: Relate gravitational force to centripetal force
Again, using the centripetal force:
mv2r=mg
Substituting for g:
mv2r=m⋅Gρ0⋅43πr3
Cancelling m:
v2r=Gρ0⋅43πr3
Rearranging gives:
v2=Gρ0⋅43π3r2
Thus, we find:
v∝r
Conclusion
The speed v as a function of distance r from the center of the system is represented by:
- For r<R: v∝r (linear relationship)
- For r≥R: v∝1√r (inverse square root relationship)
ρ={ρ0for r<R0for r≥R
M=ρ0⋅43πR3
g=GMr2=G(ρ0⋅43πR3)r2
mv2r=mg
Substituting for g:
mv2r=m⋅G(ρ0⋅43πR3)r2
Cancelling m from both sides:
v2r=G(ρ0⋅43πR3)r2
Rearranging gives:
v2=G(ρ0⋅43πR3)r
Thus, we find:
v∝1√r
M′=ρ0⋅43πr3
Thus, the gravitational field g is:
g=GM′r2=G(ρ0⋅43πr3)r2=Gρ0⋅43πr3
mv2r=mg
Substituting for g:
mv2r=m⋅Gρ0⋅43πr3
Cancelling m:
v2r=Gρ0⋅43πr3
Rearranging gives:
v2=Gρ0⋅43π3r2
Thus, we find:
v∝r
- For r<R: v∝r (linear relationship)
- For r≥R: v∝1√r (inverse square root relationship)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE5videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive)ASSERTIOIN AND REASON1videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Main (Archive)43videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)12videos
INTRODUCTION TO VECTORS & FORCES
Similar Questions
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A12R√(1Gm)B√(Gm2R)C12√(GmR)D√(4GmR) - Question 2 - Select One
Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A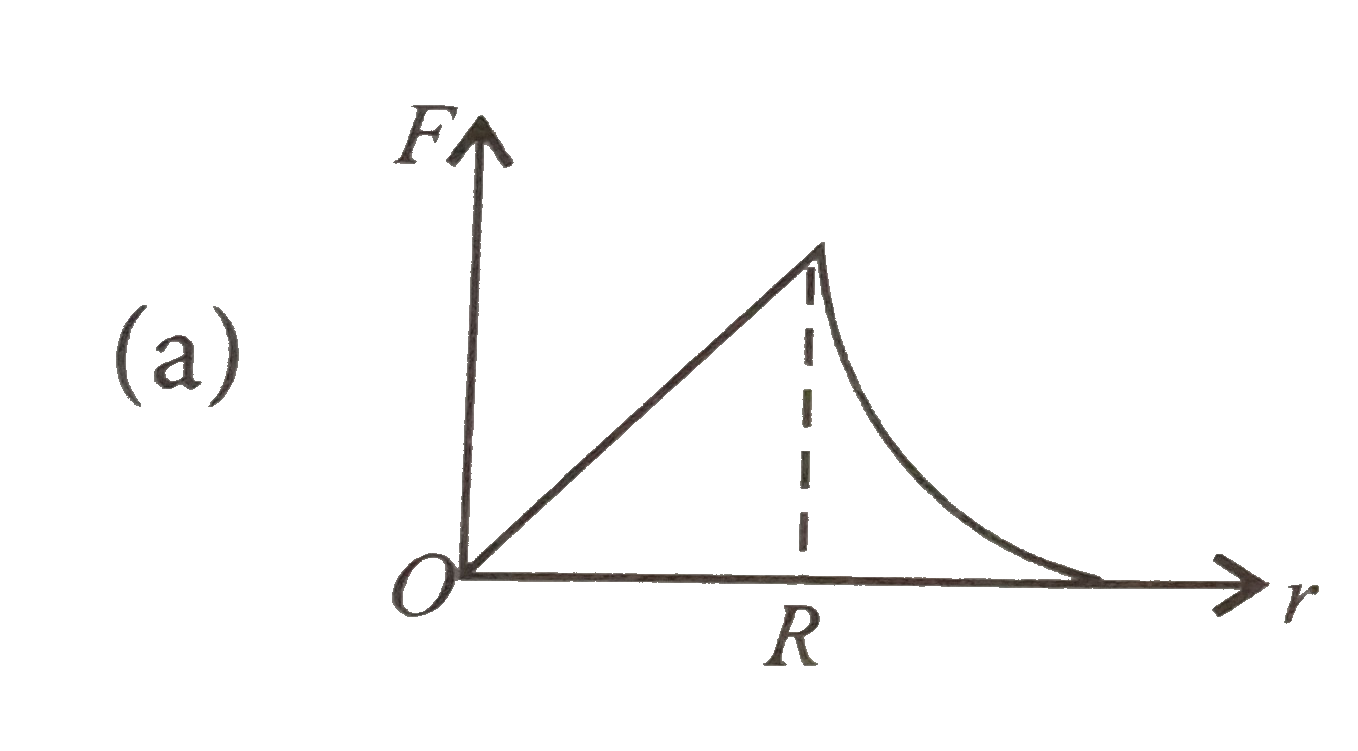 B
B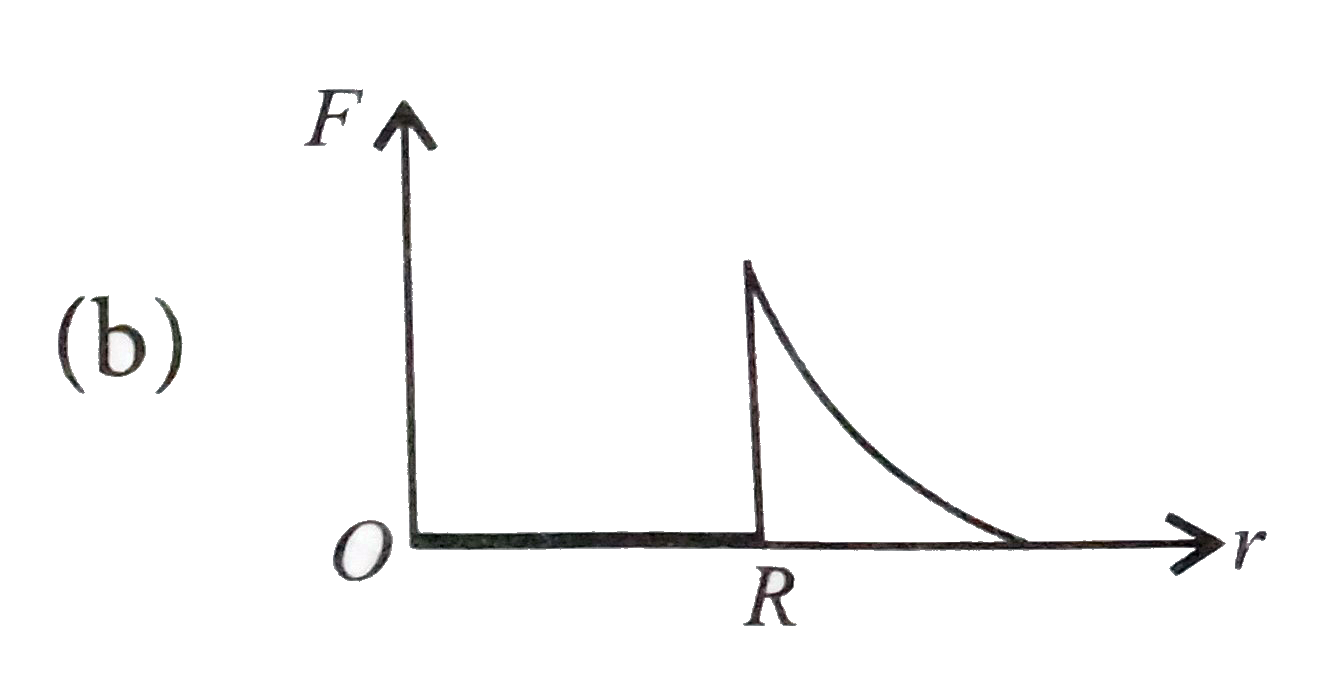 C
C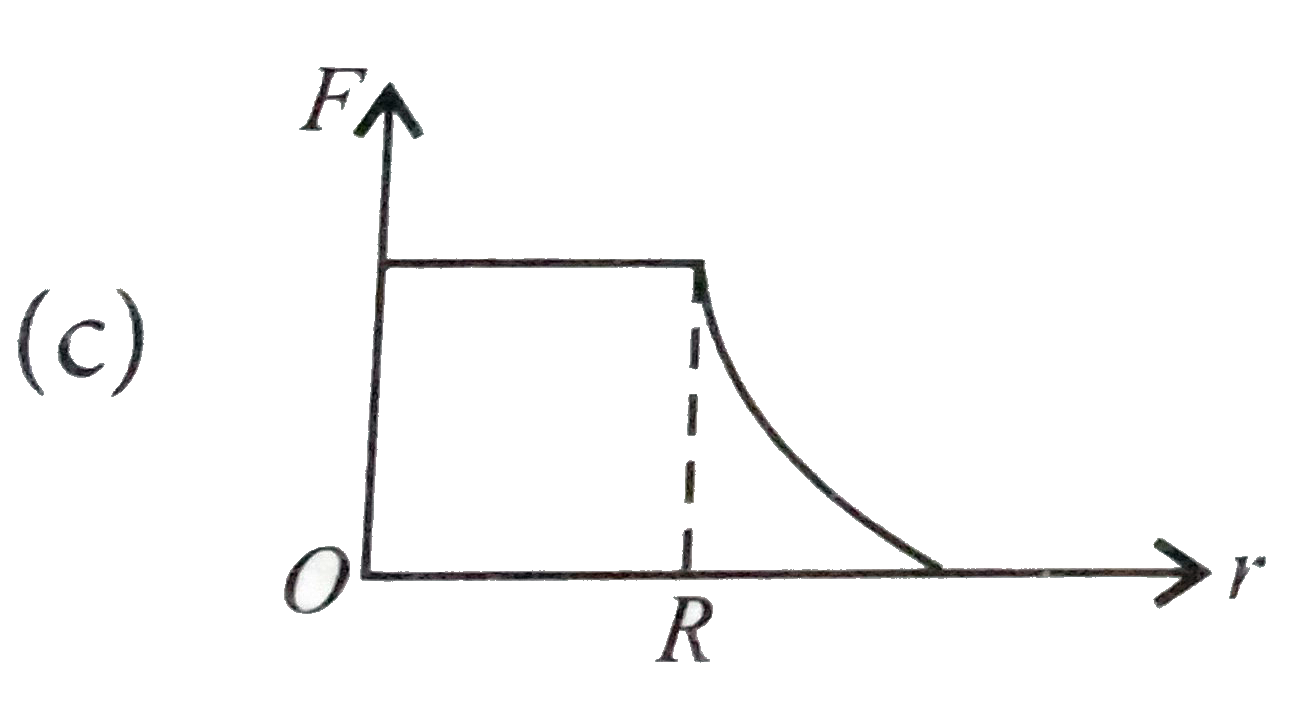 D
D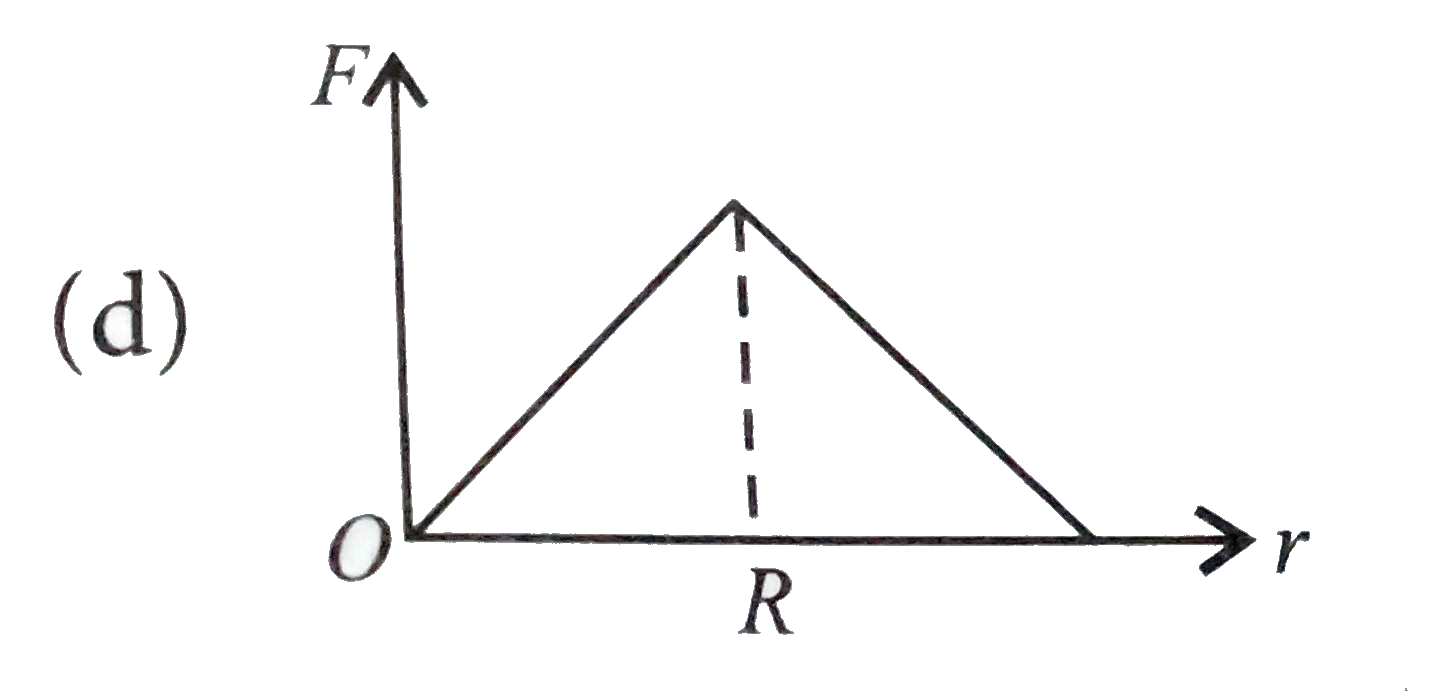
Three particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionFour particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.View SolutionThe mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
View Solution

