Let E1andE2 denotes gravitational field at distance r1andr2 from the axis of an infinitely long solid cylinder of the radius R. Which of the following must hold true ?
E1<E2 if r1<r2<R
E1>E2 if R<r1<r2
E1>E2, if r1=R−E,r2=R+E (E is positive constant <R )
All of the above
The correct Answer is:D
To solve the problem of determining the relationship between the gravitational fields E1 and E2 at distances r1 and r2 from the axis of an infinitely long solid cylinder of radius R, we can analyze the gravitational field both inside and outside the cylinder using Gauss's law.
1. Understanding the Setup:
- We have an infinitely long solid cylinder with radius R.
- We need to find the gravitational field at two different distances r1 and r2 from the axis of the cylinder.
2. Applying Gauss's Law:
- Gauss's law for gravity states that the gravitational flux through a closed surface is equal to the enclosed mass divided by G (gravitational constant).
- The gravitational field E is related to the mass enclosed by the Gaussian surface.
3. Case 1: Inside the Cylinder (r<R):
- For a point inside the cylinder, the gravitational field E is directly proportional to the distance r from the axis:
E=GMenc2πr
- Here, Menc is the mass enclosed within radius r. Since the mass density ρ is uniform, we can express Menc as:
Menc=ρ⋅Volume=ρ⋅πr2L
- Thus, the gravitational field inside the cylinder is:
E∝r
4. Case 2: Outside the Cylinder (r>R):
- For a point outside the cylinder, the gravitational field E is inversely proportional to the distance r:
E=GMtotal2πr
- Here, Mtotal is the total mass of the cylinder, which remains constant regardless of r as long as r>R.
- Thus, the gravitational field outside the cylinder is:
E∝1r
5. Comparing E1 and E2:
- If r1<R and r2<R (both points inside the cylinder), then since E∝r:
If r1<r2⇒E1<E2
- If r1>R and r2>R (both points outside the cylinder), then since E∝1r:
If r1<r2⇒E1>E2
6. Conclusion:
- The relationships derived show that:
- Inside the cylinder, the gravitational field increases with distance from the axis.
- Outside the cylinder, the gravitational field decreases with distance from the axis.
- We have an infinitely long solid cylinder with radius R.
- We need to find the gravitational field at two different distances r1 and r2 from the axis of the cylinder.
- Gauss's law for gravity states that the gravitational flux through a closed surface is equal to the enclosed mass divided by G (gravitational constant).
- The gravitational field E is related to the mass enclosed by the Gaussian surface.
- For a point inside the cylinder, the gravitational field E is directly proportional to the distance r from the axis:
E=GMenc2πr
- Here, Menc is the mass enclosed within radius r. Since the mass density ρ is uniform, we can express Menc as:
Menc=ρ⋅Volume=ρ⋅πr2L
- Thus, the gravitational field inside the cylinder is:
E∝r
- For a point outside the cylinder, the gravitational field E is inversely proportional to the distance r:
E=GMtotal2πr
- Here, Mtotal is the total mass of the cylinder, which remains constant regardless of r as long as r>R.
- Thus, the gravitational field outside the cylinder is:
E∝1r
- If r1<R and r2<R (both points inside the cylinder), then since E∝r:
If r1<r2⇒E1<E2
- If r1>R and r2>R (both points outside the cylinder), then since E∝1r:
If r1<r2⇒E1>E2
- The relationships derived show that:
- Inside the cylinder, the gravitational field increases with distance from the axis.
- Outside the cylinder, the gravitational field decreases with distance from the axis.
Similar Questions
The magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
View SolutionThe magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then:
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionThe magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M, respectively. Find the ratio of (I1)/(I2)) if r1>R and r2>R.
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
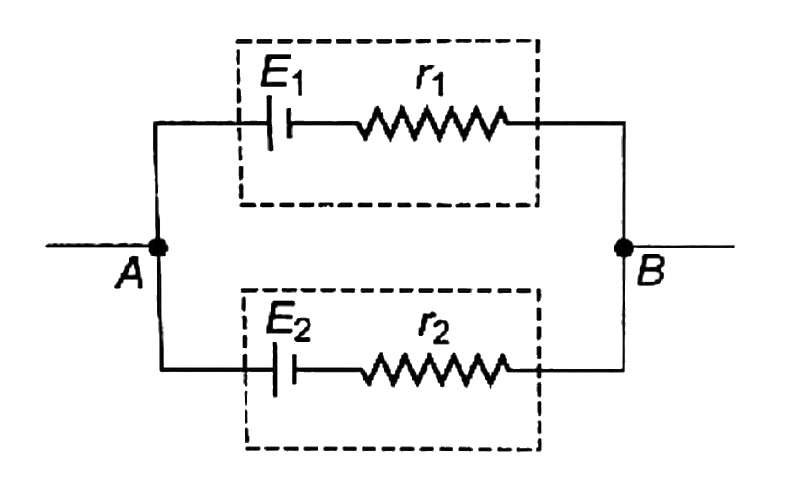
View SolutionLet E1(r), E2(r) and E3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density λ, and an infinite plane with uniform surface charge density σ. If E1(r0)=E2(r0)=E3(r0) at a given distance r0, then
View SolutionIf gravitational field Intensity is E at distance R/2 outside from then surface of a thin shell of radius R , the gravitational field intensity at distance R/2 from its centre is
View SolutionDependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by
View SolutionDependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by
View SolutionA condenser is charged using a constant current. The ratio of the magnetic fields at a distance of R/2 and R from the axis is (R is the radius of plate )
View Solution
