Distance between the centres of two stars is $10 a$ . The masses of these stars are $M$ and $16 M$ and their radit $a$ and $2 a$ respectively. A body of mass $m$ is fired straight from the surface of the larger star towards the smaller star. What should be its minimum inital speed to each the surface of the smaller star? Obtain the expression in terms of $G$ , $M$ and $a$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{3}{2}$

Let the force of attraction becomes zero at P at a distance r from bigger star.

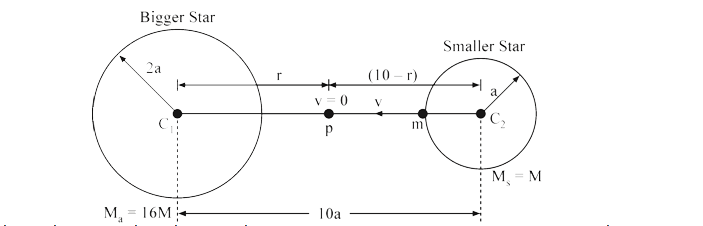
As this point gravitational field strength becomes zero or at P field due to bigger star is equal and opposite due to smaller star.
$\frac{G M_{B}}{r^{2}} = \frac{G M_{S}}{{(10 a - r)}^{2}}, \frac{16 M}{r^{2}} = \frac{M}{{(10 a - r)}^{2}} \Rightarrow r = 8 a$
Now if we fire a mass m from bigger star giving it such a velocity that is sufficient to cross point P, then later on due to more force by the star $M_{B}$ it will pull it towards itself. Now from conservation of mechanical energy of mass m from surface of larger star to point P.
$- \frac{G M_{B} M}{2 a} - \frac{G M_{S} M}{8 a} + \frac{1}{2} m v_{min}^{2} = \frac{- G M_{B} m}{8 a} - \frac{G M_{S} m}{2 a} + 0 [∵ M_{B} = 16 M M_{S} = M]$
After solving we get $v_{min} = \frac{3}{2} \sqrt{\frac{5 G M}{a}}$

|

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-GRAVITATION-JEE Advance (Archive) NUMERICAL ANSWER

Home
Ask Doubt
Profile