Distance between the centres of two stars is 10a. The masses of these stars are M and 16M and their radii a and 2a respectively. A body of mass m is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of G, M and a.
The correct Answer is:A, B, C
To solve the problem, we need to find the minimum initial speed required for a body of mass m to reach the surface of the smaller star when fired from the surface of the larger star. Let's break down the solution step by step.
Step 1: Understand the Setup
We have two stars:
- Larger star with mass M and radius a.
- Smaller star with mass 16M and radius 2a.
- The distance between the centers of the two stars is 10a.
Step 2: Identify the Forces
When the body of mass m is fired from the surface of the larger star, it will be influenced by the gravitational forces of both stars. We need to find the point where the gravitational attractions from both stars are equal.
Step 3: Determine the Distance from Each Star
Let R1 be the distance from the center of the smaller star to the point where the forces are equal, and R2 be the distance from the center of the larger star. We know:
R1+R2=10a
The gravitational force exerted by the smaller star on the body is:
F1=G⋅16M⋅mR21
And the gravitational force exerted by the larger star is:
F2=G⋅M⋅mR22
Setting these forces equal gives us:
G⋅16M⋅mR21=G⋅M⋅mR22
Step 4: Simplify the Equation
Canceling G and m from both sides, we have:
16MR21=MR22
This simplifies to:
16R22=R21
Thus,
R1=4R2
Step 5: Substitute Back into the Distance Equation
Substituting R1 into the distance equation:
4R2+R2=10a
This gives:
5R2=10a
Thus,
R2=2a
And substituting back to find R1:
R1=4R2=8a
Step 6: Calculate the Potential Energy
The potential energy at the surface of the larger star (initial position) and at the point R (where the forces are equal) can be calculated as follows:
- Potential energy at the surface of the larger star:
PEinitial=−G⋅M⋅ma
- Potential energy at the point R:
PER=−G⋅16M⋅m2a−G⋅M⋅m8a
Step 7: Set Up the Energy Conservation Equation
Using the conservation of energy:
KEinitial+PEinitial=PER
Where KEinitial=12mv2min.
Substituting the potential energies:
12mv2min−G⋅M⋅ma=−G⋅16M⋅m2a−G⋅M⋅m8a
Step 8: Solve for vmin
Rearranging gives:
12mv2min=G⋅M⋅ma−(−G⋅16M⋅m2a−G⋅M⋅m8a)
Combining terms and simplifying:
12mv2min=G⋅m(Ma+16M2a+M8a)
Step 9: Final Expression
After simplification, we find:
v2min=45GM4a
Thus,
vmin=√45GM4a
Final Answer
The minimum initial speed required for the body to reach the surface of the smaller star is:
vmin=3√52√GMa
We have two stars:
- Larger star with mass M and radius a.
- Smaller star with mass 16M and radius 2a.
- The distance between the centers of the two stars is 10a.
When the body of mass m is fired from the surface of the larger star, it will be influenced by the gravitational forces of both stars. We need to find the point where the gravitational attractions from both stars are equal.
Let R1 be the distance from the center of the smaller star to the point where the forces are equal, and R2 be the distance from the center of the larger star. We know:
R1+R2=10a
F1=G⋅16M⋅mR21
And the gravitational force exerted by the larger star is:
F2=G⋅M⋅mR22
G⋅16M⋅mR21=G⋅M⋅mR22
Canceling G and m from both sides, we have:
16MR21=MR22
This simplifies to:
16R22=R21
Thus,
R1=4R2
Substituting R1 into the distance equation:
4R2+R2=10a
This gives:
5R2=10a
Thus,
R2=2a
And substituting back to find R1:
R1=4R2=8a
The potential energy at the surface of the larger star (initial position) and at the point R (where the forces are equal) can be calculated as follows:
- Potential energy at the surface of the larger star:
PEinitial=−G⋅M⋅ma
- Potential energy at the point R:
PER=−G⋅16M⋅m2a−G⋅M⋅m8a
Using the conservation of energy:
KEinitial+PEinitial=PER
Where KEinitial=12mv2min.
12mv2min−G⋅M⋅ma=−G⋅16M⋅m2a−G⋅M⋅m8a
Rearranging gives:
12mv2min=G⋅M⋅ma−(−G⋅16M⋅m2a−G⋅M⋅m8a)
12mv2min=G⋅m(Ma+16M2a+M8a)
After simplification, we find:
v2min=45GM4a
Thus,
vmin=√45GM4a
The minimum initial speed required for the body to reach the surface of the smaller star is:
vmin=3√52√GMa
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.1
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Distance between the centres of two rings is a. The masses of these rings are M and 4M. A body of mass m is fired straight from the centre of the heavier ring. What should be its minimum initial speed to cross of lighter ring ? The radius of the both ring is R. (Assume a>>R).

View SolutionWhat is the source of energy of sun or stars ?
View SolutionTwo planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
View SolutionStar Fish is
View SolutionStar Fish is
View SolutionSea Star is
View Solution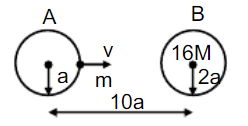
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View SolutionAlpha Centauri, our nearest star, is at a distance of
View SolutionThe radiation emitted by a star A is 10,000 times that of the sun. If the surface temperatures of the sun and the star A are 6000 K and 2000 K respectively, the ratio of the radii of the star A and the sun is
View SolutionThe radiation emitted by a star A is 10,000 times that of the sun. If the surface temperatures of the sun and the star A are 8000 K and 2000 K respectively. The ratio of the radii of the star A and the sun is
View Solution
