Equal molecules of two gases are in thermal equilibrium. If Pa,PbandVa,Vb are their respective pressures and volumes, then which of the following relation is true?
Pa≠Pb,Va=Vb
Pa=Pb,Va≠Vb
PaVa=PbVb
PaVa=PbVb
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the pressures and volumes of two gases (A and B) that are in thermal equilibrium.
1. Understanding Thermal Equilibrium:
- When two gases are in thermal equilibrium, they are at the same temperature. Therefore, we can denote the temperatures of gas A and gas B as TA=TB.
2. Applying Boyle's Law:
- Boyle's Law states that for a given mass of gas at constant temperature, the pressure (P) of the gas is inversely proportional to its volume (V). Mathematically, this can be expressed as:
P∝1V(at constant temperature)
- This implies that:
PV=constant
3. Setting Up the Relation:
- Since both gases A and B are at the same temperature, we can apply Boyle's Law to both gases:
PAVA=PBVB
- This equation indicates that the product of pressure and volume for gas A is equal to the product of pressure and volume for gas B.
4. Conclusion:
- The correct relation that holds true for the two gases in thermal equilibrium is:
PAVA=PBVB
Final Answer:
The relation that is true for the two gases in thermal equilibrium is:
PAVA=PBVB
- When two gases are in thermal equilibrium, they are at the same temperature. Therefore, we can denote the temperatures of gas A and gas B as TA=TB.
- Boyle's Law states that for a given mass of gas at constant temperature, the pressure (P) of the gas is inversely proportional to its volume (V). Mathematically, this can be expressed as:
P∝1V(at constant temperature)
- This implies that:
PV=constant
- Since both gases A and B are at the same temperature, we can apply Boyle's Law to both gases:
PAVA=PBVB
- This equation indicates that the product of pressure and volume for gas A is equal to the product of pressure and volume for gas B.
- The correct relation that holds true for the two gases in thermal equilibrium is:
PAVA=PBVB
The relation that is true for the two gases in thermal equilibrium is:
PAVA=PBVB
Similar Questions
A gas in container A is in thermal equilibrium with another gas in container B. Both contain equal masses of the two gases. Which of the following can be true ?
View SolutionTwo different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
View SolutionTwo different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
View SolutionTwo different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
View SolutionFigure shows an ideal fluid flowing through a uniform cross-sectional tube in the vertical tube with liquid velocities vA and vB and pressure PA and PB. Knowing that offers no resistance to fluid flow then which of the following is true.
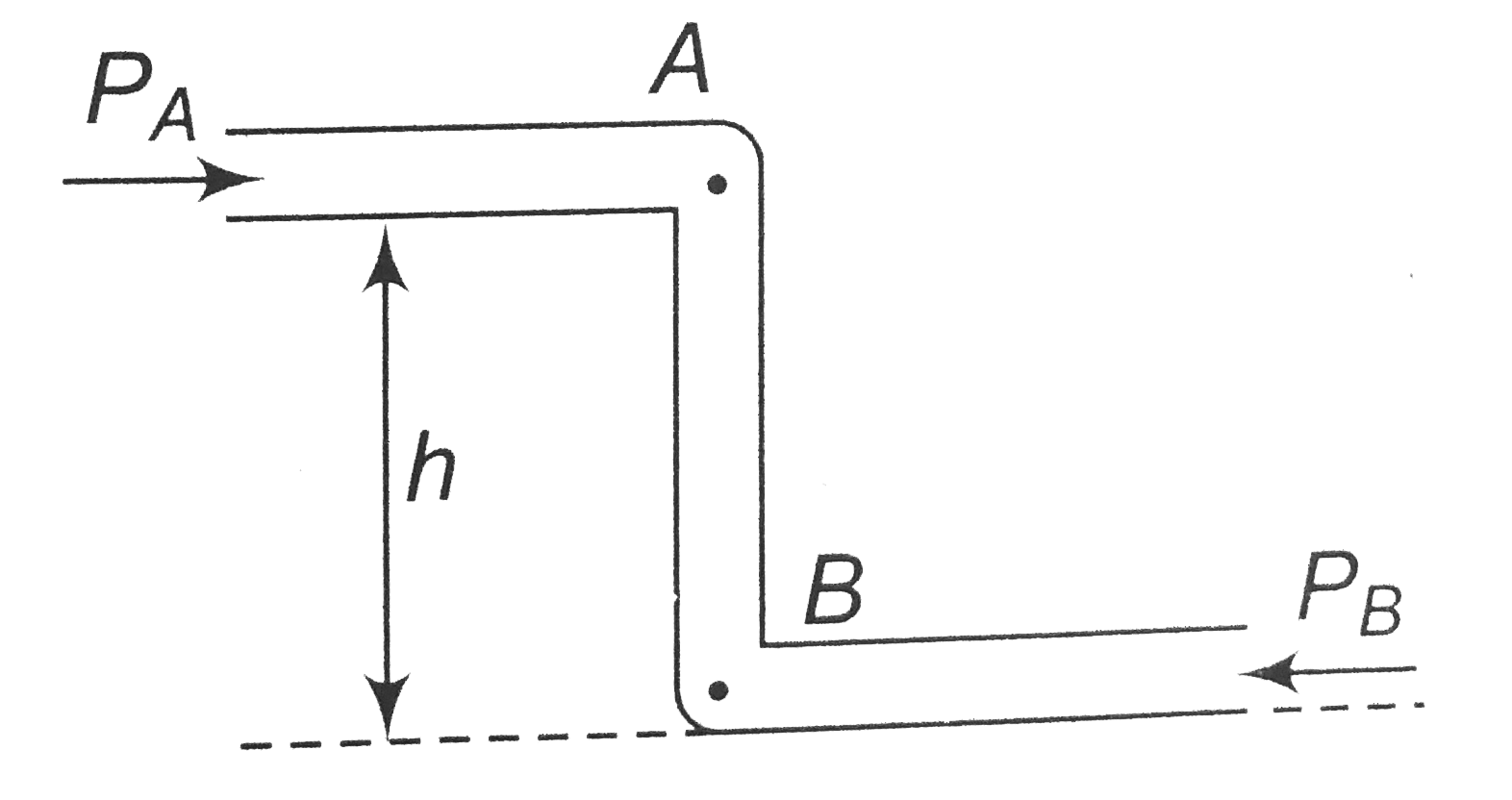 View Solution
View SolutionTwo objects A and B are moving with velocities vAandvB respectively along positive x-axis. If vA<vB then, which of the following position-time graphs is correctly showing the velocity of A and B ?
View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
AT relatively high pressures, the van der Waals' equation of state reduces toView SolutionOn an isothermal process, there are two POINTs A and B at which pressures and volumes are (2P0,V0) and (P0,2V0) respectively. If A and B are connected by a straight line, find the pressure at a POINT on this straight line at which temperature is maximum
View SolutionAn ideal fluid is flowing through the given tubes which is placed on a horizontal surface. If the liquid has velocities VA and VB and pressure PA and PB at point A and B respectively, then the correct relation is (A and B are at same height from ground level. the figure shown is as in the system is seen from the top):
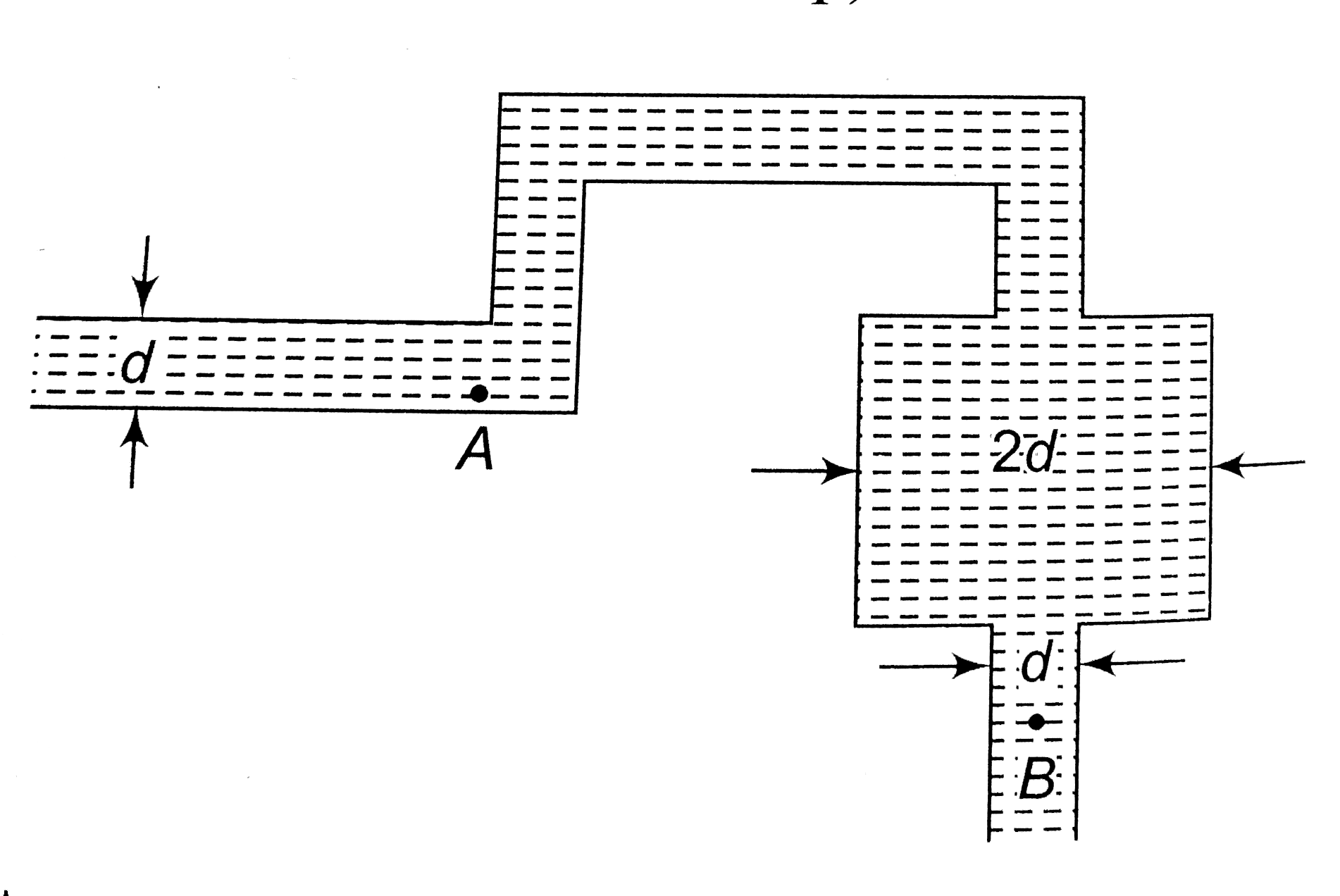 View Solution
View SolutionThe equation of state of some gases can be expressed as (P+aV2)=RθV where P is the pressure V the volume,θThe temperature and a and b are constant .The dimensional formula of a is
View Solution

