A block of mass m is attached to a spring of spring constant k is free to oscillate with angular velocity ω in a horizontal plane without friction or clamping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. the ammplitude of oscillationsin terms of ω,x0andv0 is
The displacement equation for an oscillation mass is given by:
x=Acos(ωt+θ) Where, A is the amplitude
xis the displacement
0is the phase constant
v=dxdt=−Aωsin(ωt+θ)
Velocity ,
At t=o, x=xo
xo=Acosθ=x0........(i)
And, dxdt=−v0=Aωsinθ
Asinθ=v0ω......(ii)
Squaring and adding equations (i)and (ii),we get:
A2(cos2θ+sin2θ)=x20+(v20ω2)
A=√x20+(v0ω2)
Hence, the amplitude of the resulting oscillation is √x20+(v0ω2)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE2videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (1)75videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 SHORT ANSWER TYPE - I8videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters ω,x0andv0.
View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View Solution
Knowledge Check
- Question 1 - Select One
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters ω,x0andv0.
A√v20ω2−x20B√ω2v20+x20C√x20ω2+v20D√v20ω2+x20 - Question 2 - Select One
A particle of mass (m) is attached to a spring (of spring constant k) and has a natural angular frequency ω0. An external force R(t) proportional to cosωt(ω≠ω0) is applied to the oscillator. The time displacement of the oscillator will be proportional to.
Amω20−ω2B1m(ω20−ω2)C1m(ω20+ω2)Dmω20+ω2 - Question 3 - Select One
A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
Ax=0.05sin5t mBx=0.05cos5t mCx=0.5sin5t mDx=5sin5t m
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
 View Solution
View SolutionA block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x=x0, the natural length of the spring. If the frame is given a constant horizontal accelration a0 towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
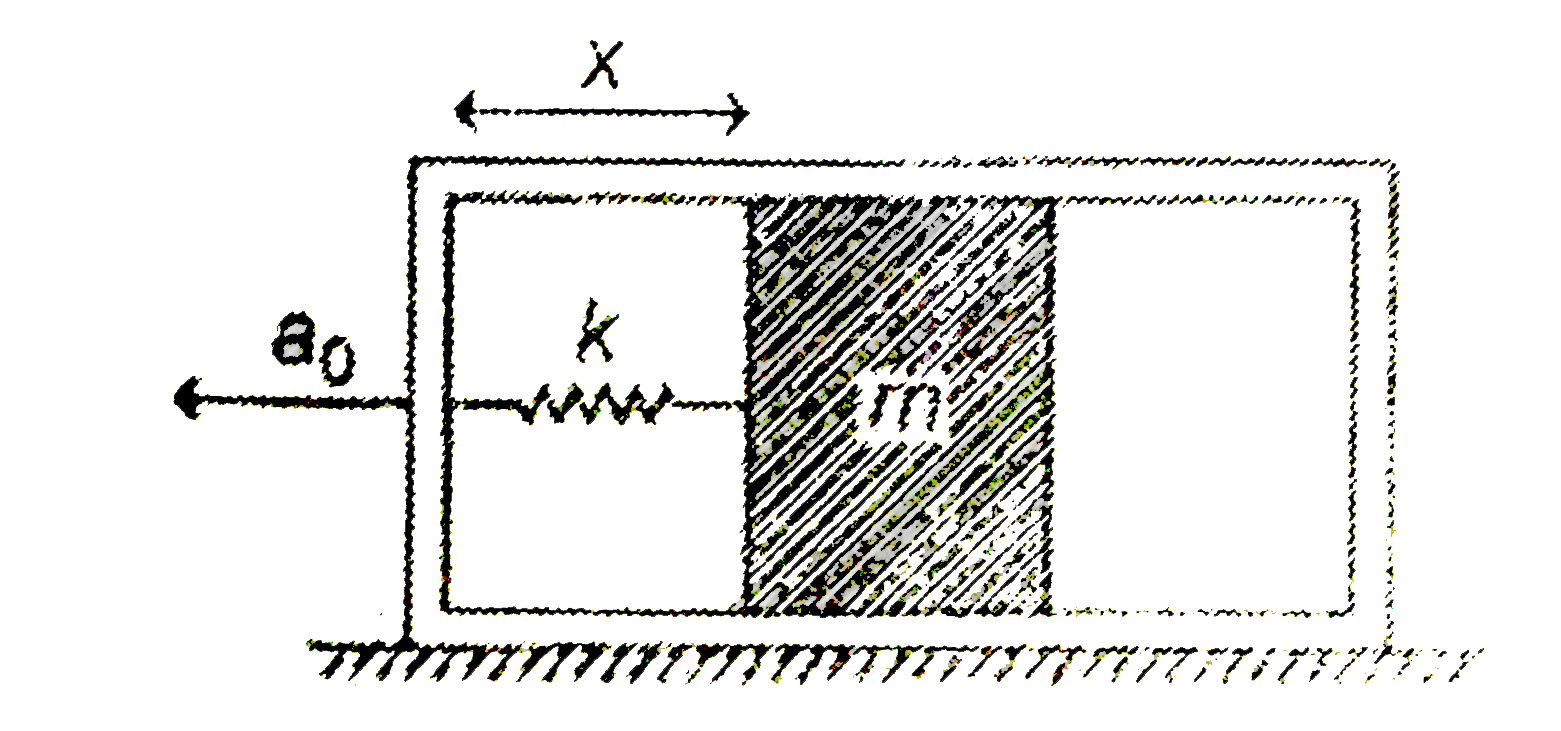 View Solution
View SolutionA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA block A of mass m connected with a spring of force constant k is executing SHM. The displacement time equation of the block is x=x0+asinωt. An identical block B moving towards negative x -axis with velocity v0 collides elastically with block A at time t=0. Then
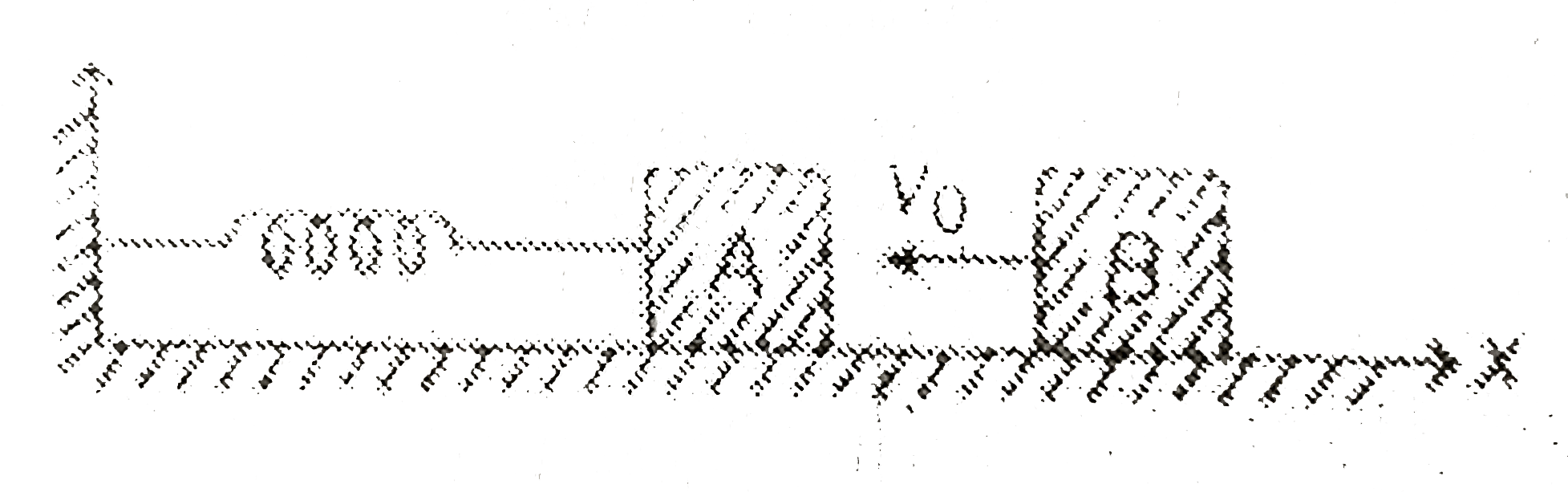 View Solution
View Solution

