The displacement of a particle varies with time according to the relation $y = a sin ω t + b c o a s ω t$ .

The motion is S.H.M. with amplitude $a^{2} + b^{2}$

The motion is S.H.M. with amplitude a+b

The motion is S.H.M. with amplitude $a^{2} + b^{2}$

The motion is S.H.M. with amplitude $\sqrt{a^{2} + b^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

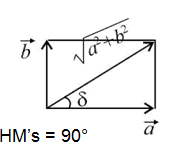
We can write
$y = \sqrt{a^{2} + b^{2}} sin (ω t + Δ)$
where $tan Δ = \frac{b}{a}$ .

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40videos
SIMPLE HARMONIC MOTION
BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56videos
SIMPLE HARMONIC MOTION
BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2videos
SIMPLE HARMONIC MOTION
BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3videos
ROTATIONAL MOTION
BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION

Knowledge Check

Question 1 - Select One
The displacement of a particle varies with time according to the relation $y = a sin ω t + b cos ω t$ .
AThe motion is oscillatory but not SHM.
BThe motion is SHM with amplitude $a + b$ .
CThe motion is SHM with amplitude $a^{2} + b^{2}$
DThe motion is SHM with amplitude $\sqrt{a^{2} + b^{2}}$ .

If the displacement of a particle varies with time as $\sqrt{x} = t + 3$
View Solution
The linear displacement (y) of a particle varies with time as $y = (a sin ω t + b cos ω t)$ . State whether the particle is executing SHM or not.
View Solution
The displacement of a particle varies according to the relation $x = 4 (cos π t + sin π t)$ . The amplitude of the particle is.
View Solution
The acceleration of a particle varies with time t seconds according to the relation $a = 6 t + 6 m s^{- 2}$ . Find velocity and position as funcitons of time. It is given that the particle starts from origin at $t = 0$ with velocity $2 m s^{- 1}$ .
View Solution
The energy E of a particle varies with time t according to the equation $E = E_{0} sin (α t) . e^{\frac{- α t}{β x}}$ , where x is displacement from mean position $E_{0}$ is energy at infinite position and $α$ and $β$ are constants .
Dimensions of $β$ are
View Solution
The energy E of a particle varies with time t according to the equation $E = E_{0} sin (α t) . e^{\frac{- α t}{β x}}$ , where x is displacement from mean position $E_{0}$ is energy at infinite position and $α$ and $β$ are constants .
Dimensional formula of $α$ is
View Solution
The energy E of a particle varies with time t according to the equation $E = E_{0} sin (α t) . e^{\frac{- α t}{β x}}$ , where x is displacement from mean position $E_{0}$ is energy at infinite position and $α$ and $β$ are constants .
Dimensions of $sin (\frac{α t}{β x})$ are
View Solution

VMC MODULES ENGLISH-SIMPLE HARMONIC MOTION -LEVEL (1)

Maximum speed of a particle in simple harmonic motion is v(max). Then ...
01:23
particle is executing SHM of amplitude A and angular frequency omega.T...
02:49
The displacement of a particle varies with time according to the relat...
05:49
Two simple harmonic motions y(1) = Asinomegat and y(2) = Acosomegat ar...
02:28
A particle is subjected to two simple harmonic motions in the same dir...
02:07
A particle is acted simultaneously by matually perpendicular simple ha...
01:45
A mass m attached to a spring of spring constant k is stretched a dist...
02:52
Frequency of a particle executing SHM is 10 Hz. The particle is suspen...
02:36
Two masses M and m are suspended together by massless spring of force ...
03:07
Three masses of 500 g, 300 g and 100 g are suspended at the end of a s...
02:31
A mass is suspended separately by two springs of spring constant k(1) ...
03:32
When a mass m is connected individually to two springs S(1) and S(2), ...
04:33
Four massless springs whose force constants are 2k, 2k, k and 2k respe...
04:55
A spring of force constant k is cut into two pieces such that one piec...
02:01
A spring of spring constant k is cut into n equal parts, out of which ...
04:15
In the figure shown the time period and the amplitude respectively, wh...
02:28
Find the time period of oscillation of block of mass m. Spring, and pu...
03:51
A pendulum has a period T for small oscillations. An obstacle is place...
03:46
The time period of a simple pendulum of length L as measured in an ele...
02:36
A pendulum suspended from the ceiling of the train has a time period o...
03:15

Home
Ask Doubt
Profile

The displacement of a particle varies with time according to the relation y=asinωt+bcoasωt.

The correct Answer is:D

We can write y=√a2+b2sin(ωt+Δ) where tanΔ=ba.

Topper's Solved these Questions

Similar Questions

Knowledge Check

The displacement of a particle varies with time according to the relation y=asinωt+bcosωt.

VMC MODULES ENGLISH-SIMPLE HARMONIC MOTION -LEVEL (1)

The displacement of a particle varies with time according to the relation $y = a sin ω t + b c o a s ω t$ .

We can write
$y = \sqrt{a^{2} + b^{2}} sin (ω t + Δ)$
where $tan Δ = \frac{b}{a}$ .

The displacement of a particle varies with time according to the relation $y = a sin ω t + b cos ω t$ .