A mass m attached to a spring of spring constant k is stretched a distance x0 from its equilibrium position and released with no initial velocity. The maximum speed attained by mass in its subsequent motion and the time at which this speed would be attained are, respectively.
(a)√kmx0 and √mk
(b)√kmx02 and π2√mk
(c)√kmx0 and π2√mk
(d)√kmx02 and π√mk
The correct Answer is:C
To solve the problem, we need to find the maximum speed attained by a mass m attached to a spring with spring constant k when it is stretched a distance x0 from its equilibrium position and released with no initial velocity. We also need to determine the time at which this maximum speed is attained.
Step 1: Determine the potential energy at the maximum displacement.
- When the mass is stretched to x0, the potential energy stored in the spring is given by:
PE=12kx20
Hint for Step 1: Remember that potential energy in a spring is calculated using the formula 12kx2.
---
Step 2: Relate potential energy to kinetic energy at the mean position.
- As the mass moves towards the mean position, all the potential energy converts into kinetic energy at the mean position (where the speed is maximum):
KE=12mv2max
- Setting the potential energy equal to the kinetic energy:
12kx20=12mv2max
Hint for Step 2: Use the principle of conservation of energy, where potential energy converts to kinetic energy.
---
Step 3: Solve for maximum speed vmax.
- Canceling 12 from both sides and rearranging gives:
kx20=mv2max
v2max=kmx20
- Taking the square root:
vmax=x0√km
Hint for Step 3: When solving for vmax, remember to take the square root of both sides.
---
Step 4: Determine the time at which maximum speed occurs.
- The time period T of the motion is given by:
T=2π√mk
- The maximum speed occurs at a quarter of the time period, which is:
t=T4=14×2π√mk=π2√mk
Hint for Step 4: Remember that the maximum speed occurs at 14 of the time period.
---
Final Answers:
- The maximum speed attained by the mass is:
vmax=x0√km
- The time at which this speed is attained is:
t=π2√mk
- When the mass is stretched to x0, the potential energy stored in the spring is given by:
PE=12kx20
- As the mass moves towards the mean position, all the potential energy converts into kinetic energy at the mean position (where the speed is maximum):
KE=12mv2max
- Setting the potential energy equal to the kinetic energy:
12kx20=12mv2max
- Canceling 12 from both sides and rearranging gives:
kx20=mv2max
v2max=kmx20
- Taking the square root:
vmax=x0√km
- The time period T of the motion is given by:
T=2π√mk
- The maximum speed occurs at a quarter of the time period, which is:
t=T4=14×2π√mk=π2√mk
- The maximum speed attained by the mass is:
vmax=x0√km
- The time at which this speed is attained is:
t=π2√mk
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)40videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE2videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m=0.1kg is connected to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the equilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
View Solution
Knowledge Check
- Question 1 - Select One
A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
Ax=0.05sin5t mBx=0.05cos5t mCx=0.5sin5t mDx=5sin5t m
A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA particle is attached to a vertical spring and is pulled down a distance 0.04m below its equilibrium position and is released from rest. The initial upward acceleration of the particle is 0.30ms−2. The period of the oscillation is
View SolutionA 5 kg collar is attached to a spring of spring constant 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beView SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
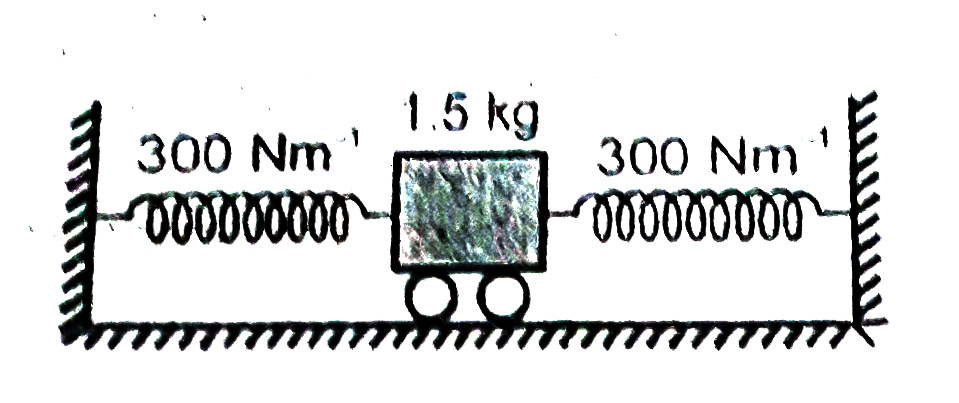 View Solution
View Solution

