A force F=-4x-8 (in N) is acting on a block where x is the position of the block in metres. The energy of oscillation is 32 J. The block oscillates between two points, out of which the value of position of one point (in metres) is an integer from 0 to 9. Find it.
The correct Answer is:6
To solve the problem step by step, we will analyze the given force, derive the necessary parameters, and find the required position of the block.
Step 1: Identify the Force Equation
The force acting on the block is given as:
F=−4x−8
Step 2: Rewrite the Force Equation
We can factor out the common term:
F=−4(x+2)
This indicates that the force is a linear function of position x and has a mean position (equilibrium position) at x=−2.
Step 3: Relate Force to Simple Harmonic Motion (SHM)
In SHM, the force can be expressed as:
F=−kx
where k is the spring constant. From our equation, we can see that:
k=4
Step 4: Calculate the Amplitude from Energy
The total mechanical energy E in SHM is given by:
E=12kA2
where A is the amplitude. We know the energy is given as 32 J:
32=12×4×A2
Step 5: Solve for Amplitude
Rearranging the equation:
32=2A2
A2=322=16
A=4
Step 6: Determine the Extreme Positions
The mean position is at x=−2, and the amplitude is 4. Therefore, the extreme positions (maximum and minimum) can be calculated as:
- Maximum position: −2+4=2
- Minimum position: −2−4=−6
Step 7: Identify the Range of Oscillation
The block oscillates between −6 and 2. We need to find the integer position within the range of 0 to 9.
Step 8: Conclusion
The integer position from 0 to 9 that the block oscillates to is:
Position=2
Thus, the final answer is:
The integer position is 2.
---
The force acting on the block is given as:
F=−4x−8
We can factor out the common term:
F=−4(x+2)
This indicates that the force is a linear function of position x and has a mean position (equilibrium position) at x=−2.
In SHM, the force can be expressed as:
F=−kx
where k is the spring constant. From our equation, we can see that:
k=4
The total mechanical energy E in SHM is given by:
E=12kA2
where A is the amplitude. We know the energy is given as 32 J:
32=12×4×A2
Rearranging the equation:
32=2A2
A2=322=16
A=4
The mean position is at x=−2, and the amplitude is 4. Therefore, the extreme positions (maximum and minimum) can be calculated as:
- Maximum position: −2+4=2
- Minimum position: −2−4=−6
The block oscillates between −6 and 2. We need to find the integer position within the range of 0 to 9.
The integer position from 0 to 9 that the block oscillates to is:
Position=2
The integer position is 2.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
A force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
View SolutionIn the given arrangement the block is released from the position where the spring is unstretched. The speed of the block when it has descended through 2cm is x10. Find the value of x.

View SolutionDistance between two point (8,−4) and (0,a) is 10. All the values are in the same unit of length. Find the positive value of a.
View SolutionPassage IX) For SHM to take place force acting on the body should be proportional to -x or F = -kx. If A be the amplitude then energy of oscillation is 12kA2
Force acting on a block is F = ( − 4 x + 8 ) .
Here F is in Newton and x the position of block on x-axis in meter If energy of osciallation is 18 J, between what points the block will oscillate?
View SolutionThe kinetic energy of a particle executing shm is 32 J when it passes through the mean position. If the mass of the particle is.4 kg and the amplitude is one metre, find its time period.
View SolutionPassage IX) For SHM to take place force acting on the body should be proportional to -x or F = -kx. If A be the amplitude then energy of oscillation is 12kA2
Force acting on a block is F=(−4x+8). Here F is in Newton and x the position of block on x-axis in meter
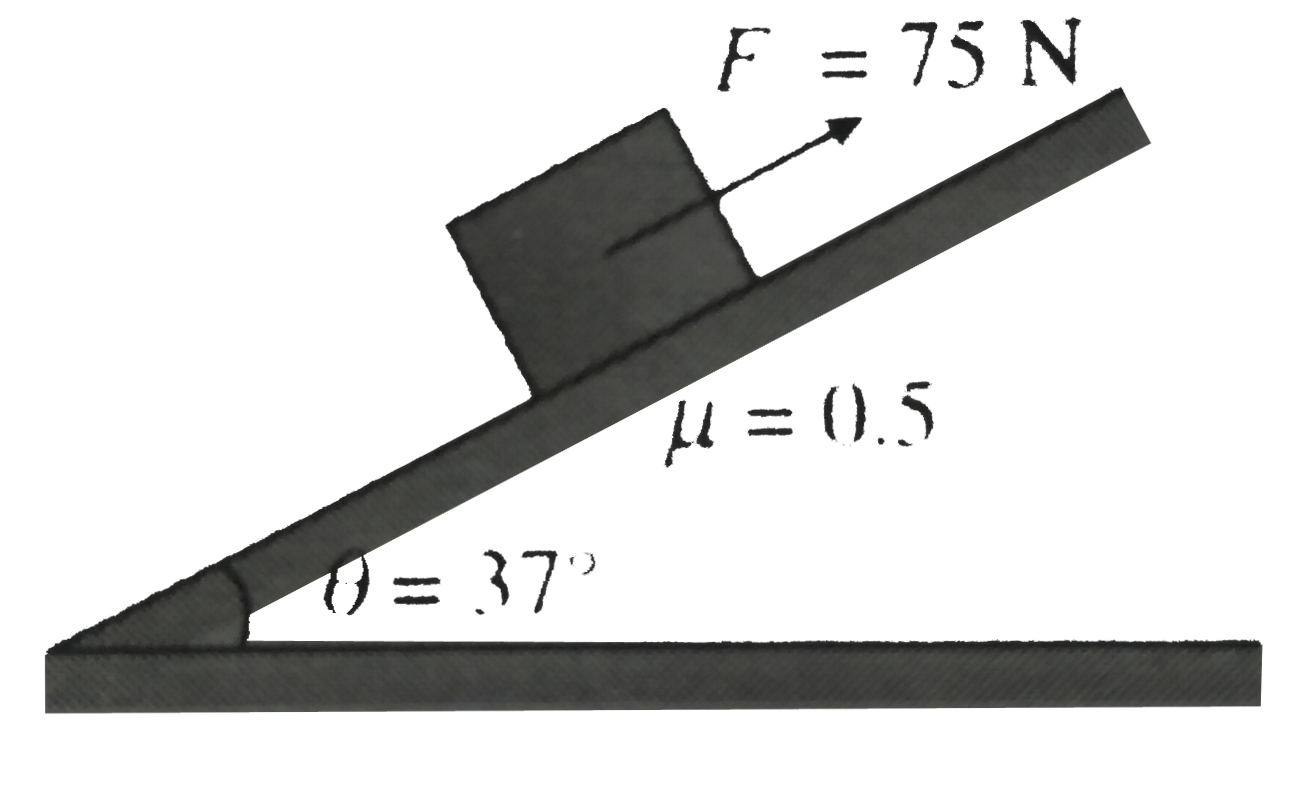
View SolutionA block of mass M=10kg is placed inclined plane , inclined at angle θ=37∘ with horizontal The coefficient of friction between the block and inclined is μ=0.5
a. Calculate the acceleration of the block when it is released
b. Now a force F=75N is appling on block as shown find out the acceleration of the block If the block is initially at rest .
c. In case (b), how much force should be added to 75N force so that block the starts to move up the incline.
d. In case (b), what is the minimum force by which 75N force should be replaced with so that the block does not move?

View SolutionA block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
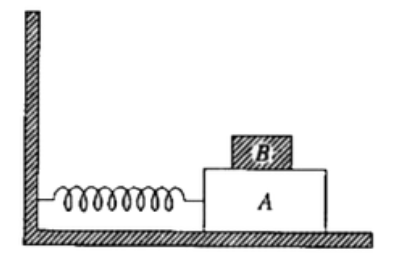
View SolutionIn Fig. A is a large block which executes shm by sliding across a frictionless surface with a frequency n. The block B is at rest on the surface of the block μs The coefficient of static friction between the two is H. Find the maximum amplitude of oscillation of the system so that the block B does not slip.
View SolutionA block of mass m is slowly carried on a inclined plane by a force F which always acts along the tangent to the plane. If the co-efficient of friction between the block and incline be μ, then work done by force of friction while carrying block from bottom of the plane to the top will be :
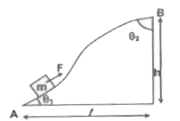
A. dependent on the actual shape of the path between point A and B.
B. will have a total positive value
C. will not change if force F is not applied along the tangent to the plane always.
D. independent of the actual shape of the path between points A and B.
View Solution
