The angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
(a)increases by 1%
(b)increases by 8%
(c)decreased by 1%
(d)decrease by 8%
The correct Answer is:A
To solve the problem step by step, we will analyze the given information and derive the required change in the time period of the damped oscillator compared to the undamped oscillator.
Step 1: Understand the given formula for angular frequency
The angular frequency of a damped oscillator is given by:
ω=√km−r24m2
where:
- k is the spring constant,
- m is the mass of the oscillator,
- r is the damping constant.
Step 2: Identify the undamped angular frequency
The angular frequency of an undamped oscillator (ω0) is given by:
ω0=√km
Step 3: Relate the time periods
The time period T of the damped oscillator is related to its angular frequency by:
T=2πω
For the undamped oscillator, the time period T0 is:
T0=2πω0
Step 4: Substitute the expressions for angular frequencies
Substituting the expressions for ω and ω0:
T=2π√km−r24m2
T0=2π√km
Step 5: Find the change in time period
To find the change in time period T−T0, we can express T in terms of T0:
T=T0⋅
⎷kmkm−r24m2
Step 6: Substitute the ratio given in the problem
We are given that:
r2mk=0.08(8%)
This implies:
r2=0.08mk
Step 7: Substitute into the expression for T
Substituting r2 into the expression for T:
T=T0⋅
⎷kmkm−0.08mk4m2
=T0⋅
⎷kmkm−0.02km
=T0⋅
⎷kmkm(1−0.02)
=T0⋅√11−0.02=T0⋅√10.98
Step 8: Calculate the percentage change in time period
The percentage change in time period is given by:
T−T0T0×100=(√10.98−1)×100
Calculating √10.98:
√10.98≈1.0102
Thus,
T−T0T0×100≈(1.0102−1)×100≈1.02%
Final Answer
The change in the time period compared to the undamped oscillator is approximately 1% increase.
The angular frequency of a damped oscillator is given by:
ω=√km−r24m2
where:
- k is the spring constant,
- m is the mass of the oscillator,
- r is the damping constant.
The angular frequency of an undamped oscillator (ω0) is given by:
ω0=√km
The time period T of the damped oscillator is related to its angular frequency by:
T=2πω
For the undamped oscillator, the time period T0 is:
T0=2πω0
Substituting the expressions for ω and ω0:
T=2π√km−r24m2
T0=2π√km
To find the change in time period T−T0, we can express T in terms of T0:
T=T0⋅
⎷kmkm−r24m2
We are given that:
r2mk=0.08(8%)
This implies:
r2=0.08mk
Substituting r2 into the expression for T:
T=T0⋅
⎷kmkm−0.08mk4m2
=T0⋅
⎷kmkm−0.02km
=T0⋅
⎷kmkm(1−0.02)
=T0⋅√11−0.02=T0⋅√10.98
The percentage change in time period is given by:
T−T0T0×100=(√10.98−1)×100
Calculating √10.98:
√10.98≈1.0102
Thus,
T−T0T0×100≈(1.0102−1)×100≈1.02%
The change in the time period compared to the undamped oscillator is approximately 1% increase.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
For the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
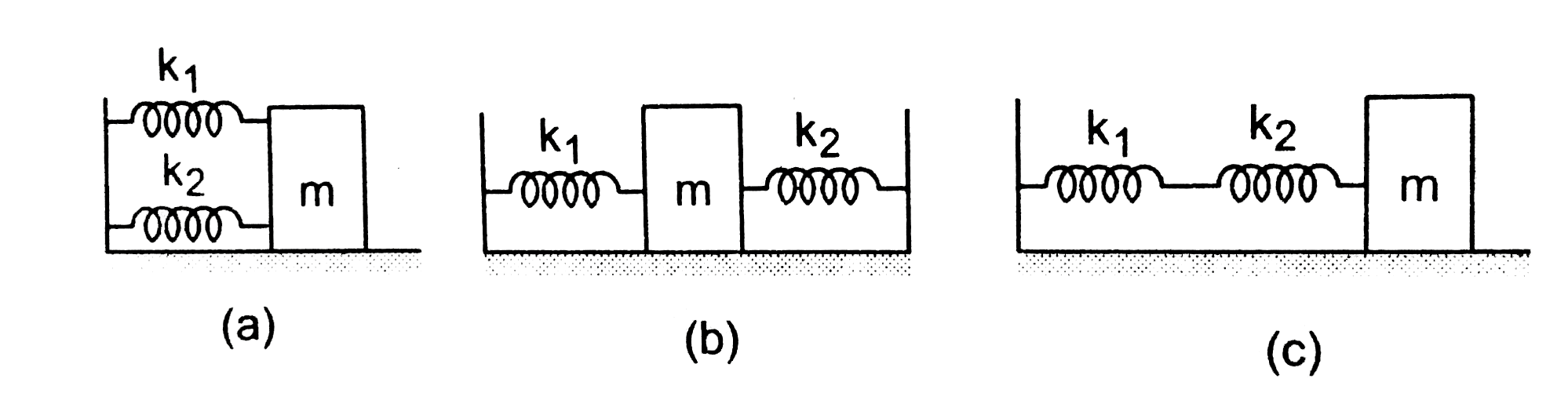
View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
For the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
The period of oscillation

View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionThe velocity of the particle of mass m as a function of time t is given by v=Aω.cos[√Kmt] , where A is amplitude of oscillation. The dimension of AK is
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1 and k2. The time period of the suspended mass will be
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionFor the damped oscillator shown in previous figure, k=180Nm−1 and the damping constant b is 40gs−1 .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than √km).
Hint :T=2π√mk
View Solution
