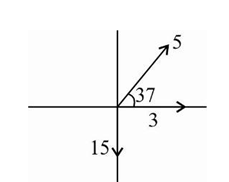
The resultant amplitude due to superposition of three simple harmonic motions x1=3sinωt,
x2=5sin(ωt+37∘) and x3=−15cosωt is
18
10
12
none of
The correct Answer is:D
x1=3sinωt
x2=5sin(ωt+37∘)
x3=15sin(ωt+π+π2)
AR=√A2x+A2y=√(7)2+(12)2=√49+144=√193
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (1)
75 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View Solutionx1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View SolutionFind the displacement equation of the simple harmonic motion obtained by combining the motion.
x1=2sinωt, x2=4sin(ωt+π6) and x3=6sin(ωt+π3)
View SolutionIf i1=3sinωtand(i2)=4cosωt, then (i3) is

View SolutionDetermine resultant amplitude after super position of given four waves with help of phasor diagram. y1=15sinωtmm,y2=9sin(ωt−π/2)mm,y3=7sin(ωt+π/2)mm & y4=13sinωtmm.
View SolutionA partical is subjucted to two simple harmonic motions
x1=A1sinωt
and x2=A2sin(ωt+π/3)
Find(a) the displacement att=0, (b) the maximum speed of the partical and ( c) the maximum acceleration of the partical.
View SolutionTwo simple harmonic motions given by, x=asin(ωt+δ) and y=asin(ωt+δ+π2) act on a particle will be
View SolutionThe equation of the resultant motion of the number of simple harmonic motions is Ec=(1+Ksinω2t)sinω1t. The number of simple harmonic components is/are.
View SolutionTwo particle AandB execute simple harmonic motion according to the equation y1=3sinωt and y2=4sin[ωt+(π/2)]+3sinωt. Find the phase difference between them.
View SolutionFind the resultant amplitude and the phase difference between the resultant wave and the first wave , in the event the following waves interfere at a point , y1=(3cm)sinωt,
y2=(4cm)sin(ωt+π2),y3=(5cm)sin(ωt+π)
View Solution
