A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
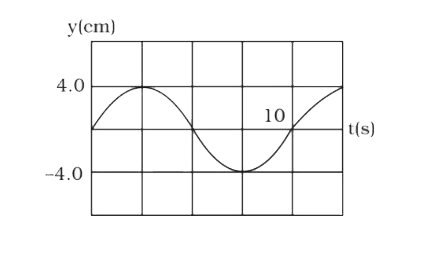
Q. The velocity of propagation of the wave is ?
−2cm/s
+2cm/s
+1.5cm/s
−2.5cm/s
The correct Answer is:D
Wave equation,
y=Asin(kx−ωt+ϕ)=4sin[2π20x−2π×0.1t+ϕ]
At t=0, x=0, y=0
⇒ϕ=0 or π
But at position x=0 as time progresses, particle starts moving along positive y-direction
∴ϕ=π satisfies
∴Equationn of wave will be y=4sin(π10x−0.2πt+π), x in cm and t is sec.
∴Particle-velocity
vp(x,y)=δyδt=4cos(π10x−0.2πt+π)×(0.2π)
∴vp(0,5)=4cos(π10×0−0.2π×5+π)×(−0.2π)=−0.8π=−2.5cm/s
Topper's Solved these Questions
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAIN ARCHIVE LEVEL 1
56 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2
32 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - LEVEL-1
75 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
Similar Questions
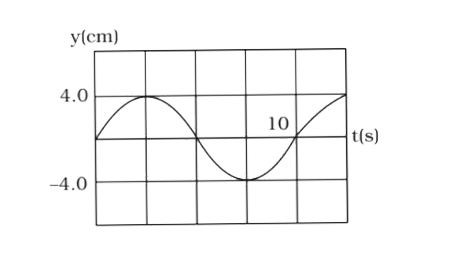
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View Solution
The velcocity displacement graph of a particle moving along a straight line is shown in figure. The velocity as function of x(0≤x≤1) is
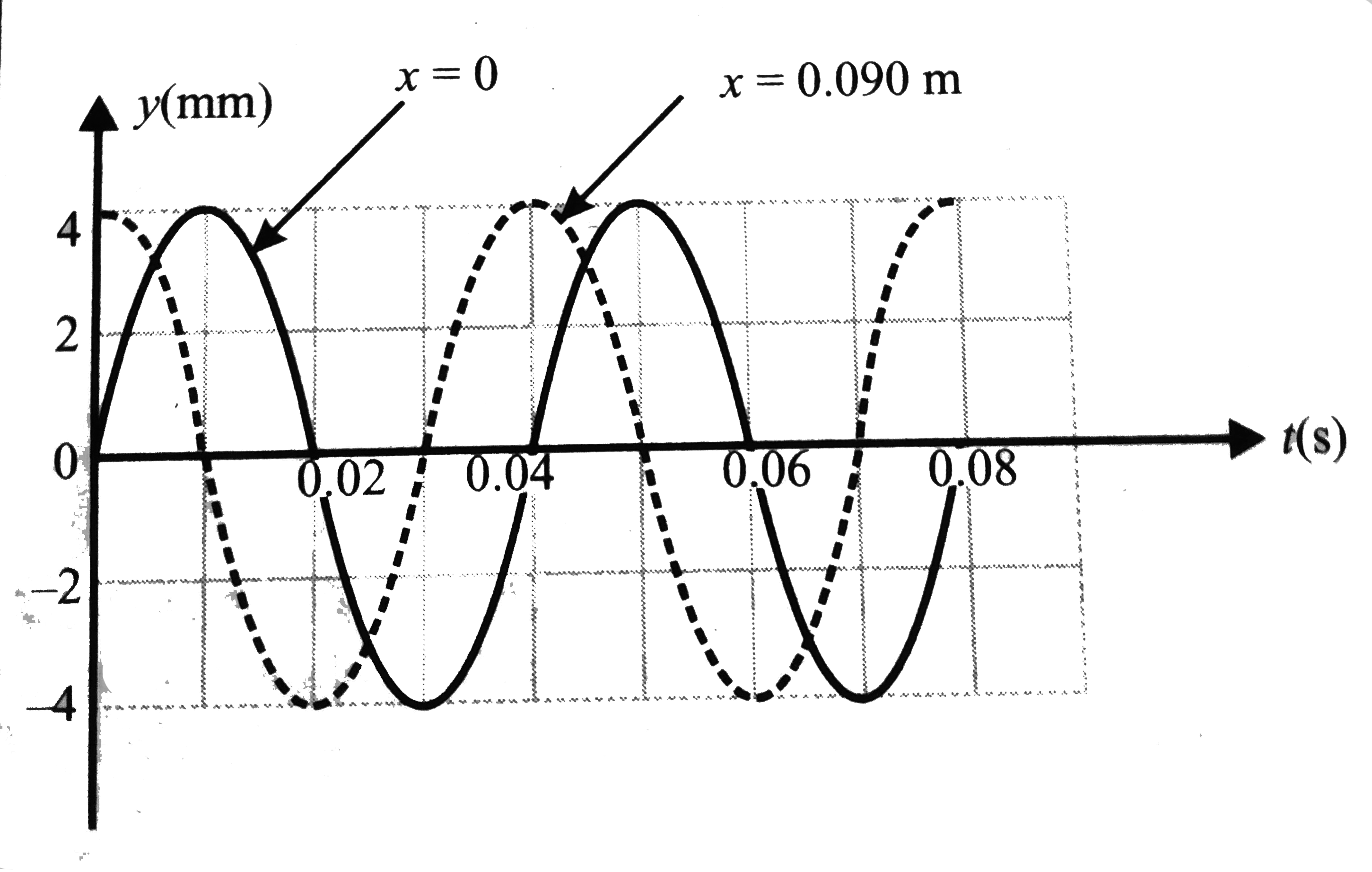
View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
View SolutionA transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
View SolutionA transverse sinusoidal wave of amplitude A, wavelength λ and frequency f is travelling along a stretch string. The maximum speed of any point on the string is v10, where, V is the velocity of wave propagation. If A=10−3m,andV=10ms−1, then λ and f are given by
View SolutionA simple harmonic plane wave propagatees along x-axis in a medium. The displacement of the particle as a function of time is shown in figure, for x=0(curve 1) and x=7 (curve 2)
The two particle are with a span of onewavelength.
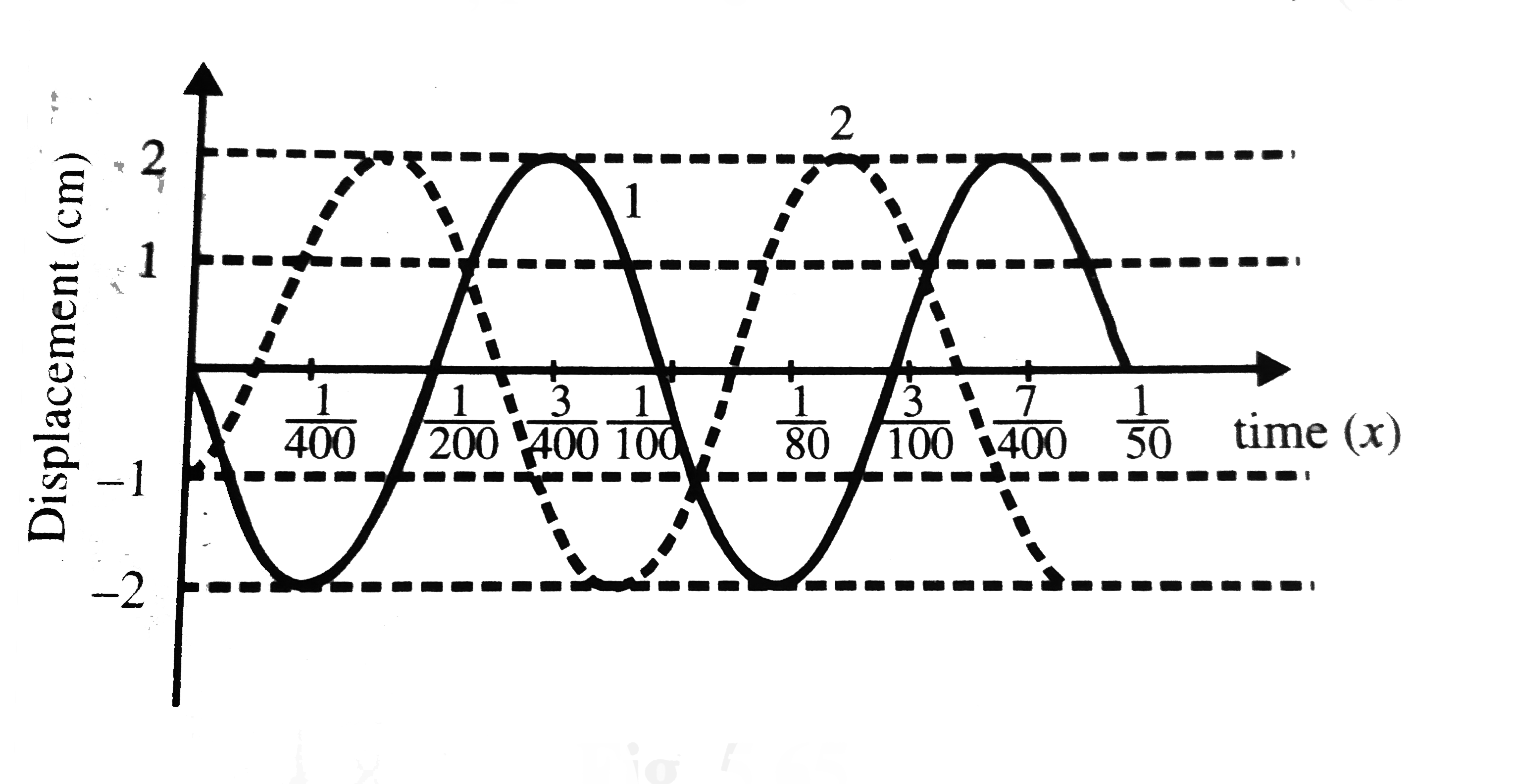
The wavelength of the wave is
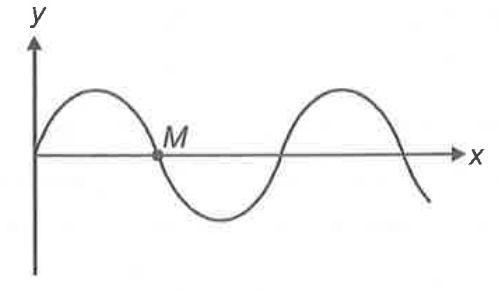
View SolutionA transverse wave is travelling along a string from right to left. The figure represents the shape of the string at the given instant. A point M has a velocity
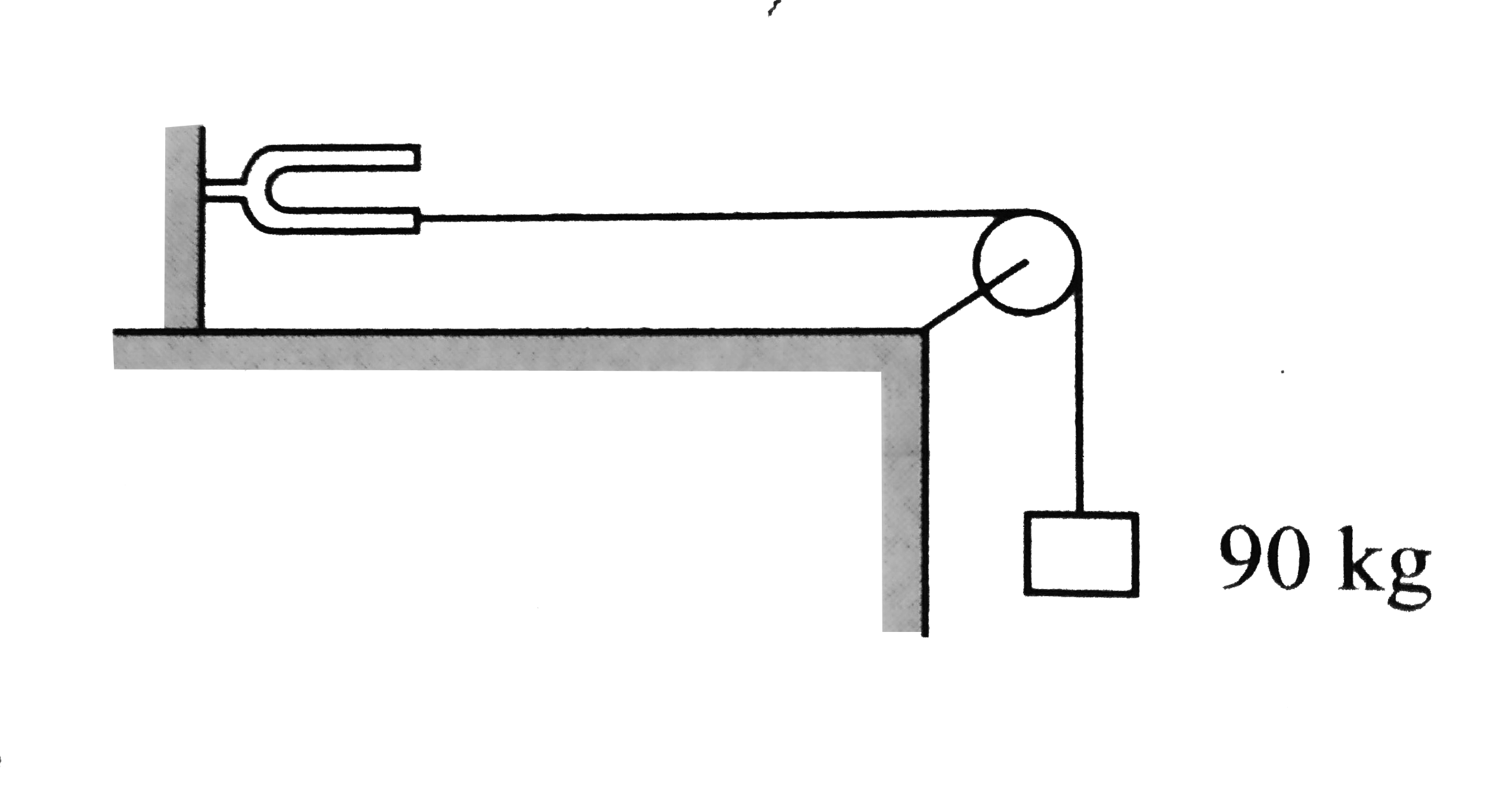
View SolutionOne end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
View Solution
