P, Q and R are three balloons ascending with velocities U, 4U and 8U respectively. If stones of the same mass be dropped from each, when they are at the same height, then
P
Q
R
Three stones take equal time
The correct Answer is:A
To solve the problem, we need to analyze the situation where three balloons (P, Q, and R) are ascending with different velocities and stones are dropped from each balloon at the same height. We will determine which stone reaches the ground first.
1. Identify the velocities of the balloons:
- Balloon P ascends with velocity U.
- Balloon Q ascends with velocity 4U.
- Balloon R ascends with velocity 8U.
2. Define the motion of the stones:
- When a stone is dropped from a balloon, it will have an initial upward velocity equal to the velocity of the balloon at the moment of release.
- Therefore, the initial velocities of the stones when dropped are:
- Stone from P: U
- Stone from Q: 4U
- Stone from R: 8U
3. Set up the equations of motion:
- The stones are subject to gravitational acceleration g acting downwards. We will use the equation of motion:
h=ut+12(−g)t2
- Here, h is the height from which the stones are dropped (which we will take as negative since it is downward), u is the initial velocity of the stone, and t is the time taken to reach the ground.
4. Write the equations for each stone:
- For the stone from balloon P:
−h=Ut−12gt2
- For the stone from balloon Q:
−h=4Ut−12gt2
- For the stone from balloon R:
−h=8Ut−12gt2
5. Rearranging the equations:
- Rearranging gives us:
12gt2−Ut=h(for P)
12gt2−4Ut=h(for Q)
12gt2−8Ut=h(for R)
6. Solve for time t:
- For each equation, we can solve for t using the quadratic formula. The general form is:
at2+bt+c=0
- For the stone from P:
12gt2−Ut+h=0
- The roots will give us the time taken for each stone to reach the ground.
7. Compare the times:
- The time taken t is inversely related to the initial velocity of the stone. The higher the initial velocity, the longer it will take to reach the ground.
- Since U<4U<8U, we conclude:
- tP<tQ<tR
8. Conclusion:
- The stone dropped from balloon P will reach the ground first, followed by the stone from Q, and finally the stone from R.
Final Answer:
The stone dropped from balloon P reaches the ground first.
- Balloon P ascends with velocity U.
- Balloon Q ascends with velocity 4U.
- Balloon R ascends with velocity 8U.
- When a stone is dropped from a balloon, it will have an initial upward velocity equal to the velocity of the balloon at the moment of release.
- Therefore, the initial velocities of the stones when dropped are:
- Stone from P: U
- Stone from Q: 4U
- Stone from R: 8U
- The stones are subject to gravitational acceleration g acting downwards. We will use the equation of motion:
h=ut+12(−g)t2
- Here, h is the height from which the stones are dropped (which we will take as negative since it is downward), u is the initial velocity of the stone, and t is the time taken to reach the ground.
- For the stone from balloon P:
−h=Ut−12gt2
- For the stone from balloon Q:
−h=4Ut−12gt2
- For the stone from balloon R:
−h=8Ut−12gt2
- Rearranging gives us:
12gt2−Ut=h(for P)
12gt2−4Ut=h(for Q)
12gt2−8Ut=h(for R)
- For each equation, we can solve for t using the quadratic formula. The general form is:
at2+bt+c=0
- For the stone from P:
12gt2−Ut+h=0
- The roots will give us the time taken for each stone to reach the ground.
- The time taken t is inversely related to the initial velocity of the stone. The higher the initial velocity, the longer it will take to reach the ground.
- Since U<4U<8U, we conclude:
- tP<tQ<tR
- The stone dropped from balloon P will reach the ground first, followed by the stone from Q, and finally the stone from R.
The stone dropped from balloon P reaches the ground first.
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 2
65 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)
19 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
B1,B2, and B3, are three balloos ascending with velocities v, 2v, and 3v, respectively, If a bomb is dropped from each when they are at the same height, then.
View SolutionTwo bodies of masses m1, and m2, moving with velocity u1, and u2, respectively in the same direction collide with each other elastically. Calculate their velocities after the collision. Discuss what happens when
(i) Both the colliding bodies have the same mass.
(ii) One of the bodies is initially at rest.
(iii) A light body collides with a heavy body at rest
(iv) A heavy body collides with a light body at rest
View Solution
Knowledge Check
A body dropped from a height h with initial velocity zero, strikes the ground with a velocity 3 m/s. Another body of same mass dropped from the same height h with an initial velocity of 4m/s. Find the final velocity of second mass with which it strikes the ground.
A3ms−1B4ms−1C5ms−1D12ms−1
A balloon rises with uniform velocity of 10ms−1. When the balloon is at a height of 75 m if a stone is dropped from it the time taken by it to reach the ground is
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
7. After 10 s of the start of motion of both objects A and B, find the value of velocity of A if uA=6ms−1,uB=12ms−1 and at T velocity of A is 8ms−1andT=4s
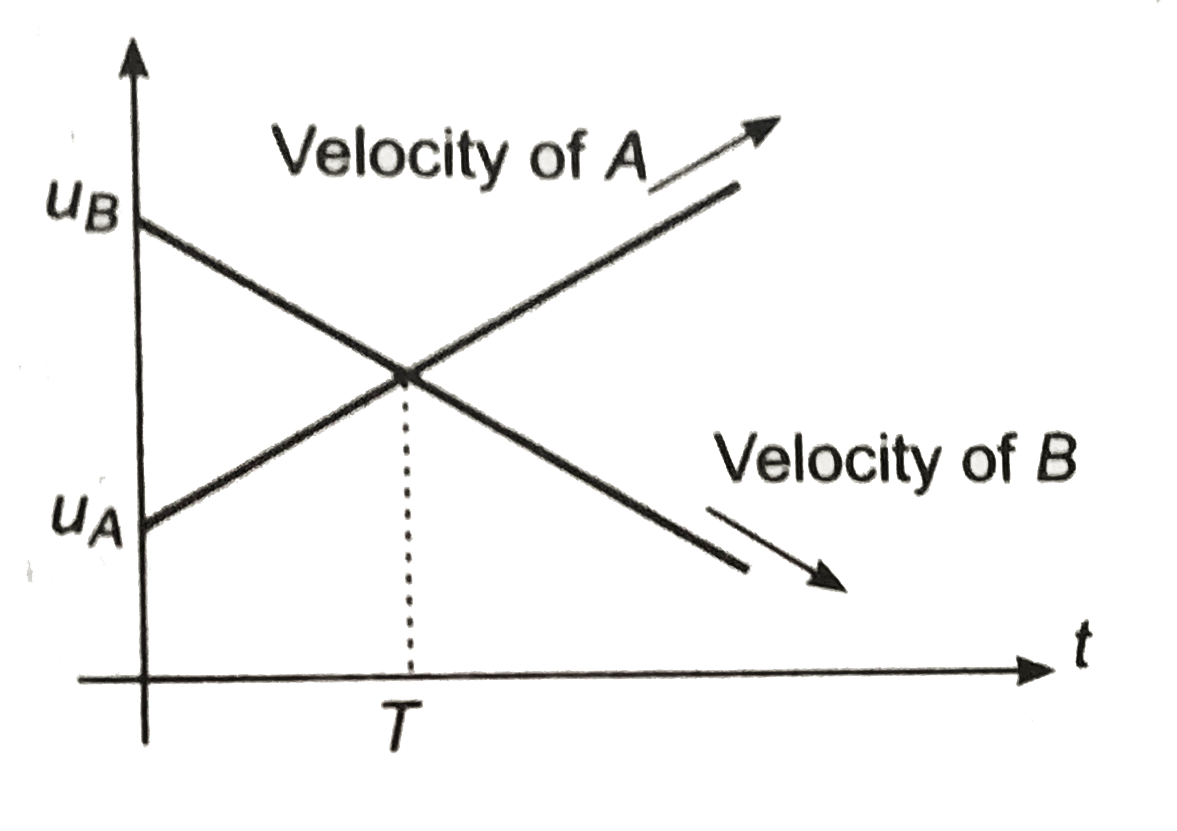
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
6. Let vAandvB be the velocities of the particles A and B respectively at the moment A and B meet after start of the motion. If uA=5ms−1anduB=15ms−1, then the magnitude of the difference of velocities vAandvB is
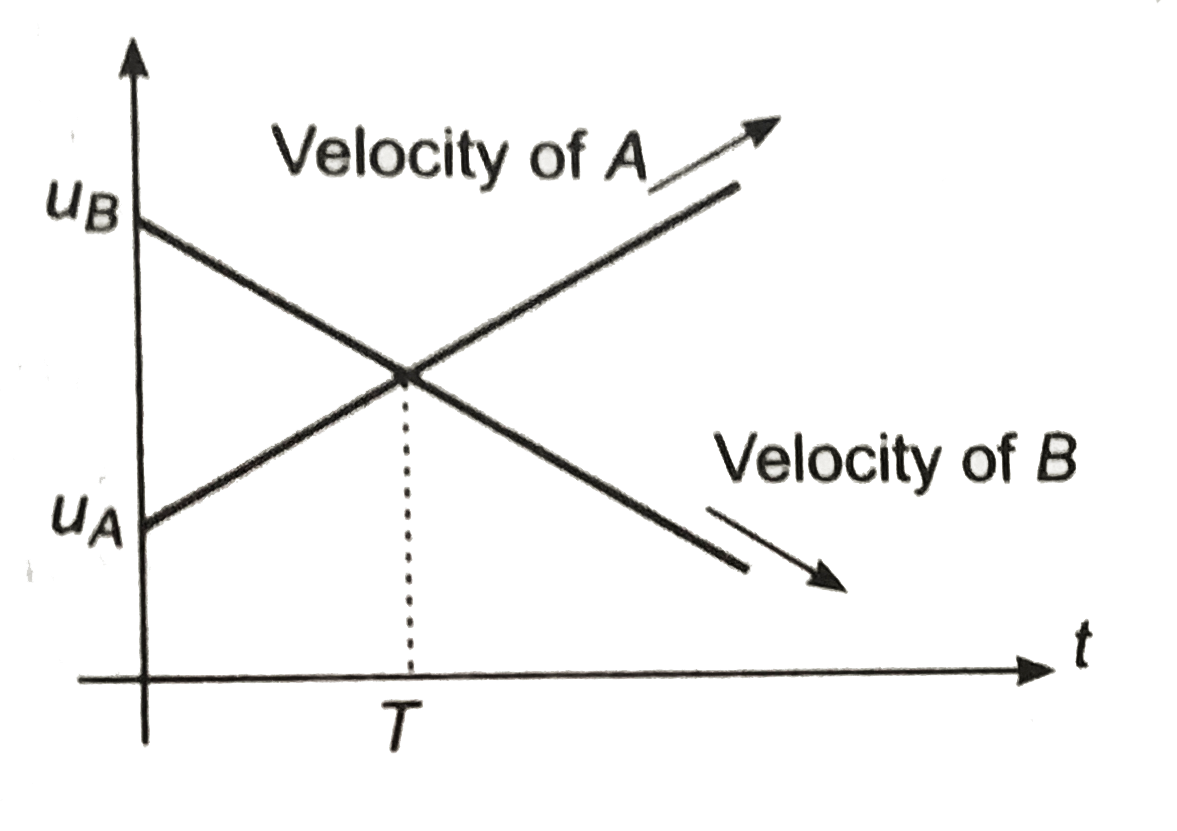
View SolutionA stone is dropped from a balloon going up with a uniform velocity of 5.0 m/s. If the balloon was 50 m high when the stone was dropped, find its height when the stone hits the ground. Take g=10ms2.
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
5. If the value of T is 4 s, then the time after which A will meet B is
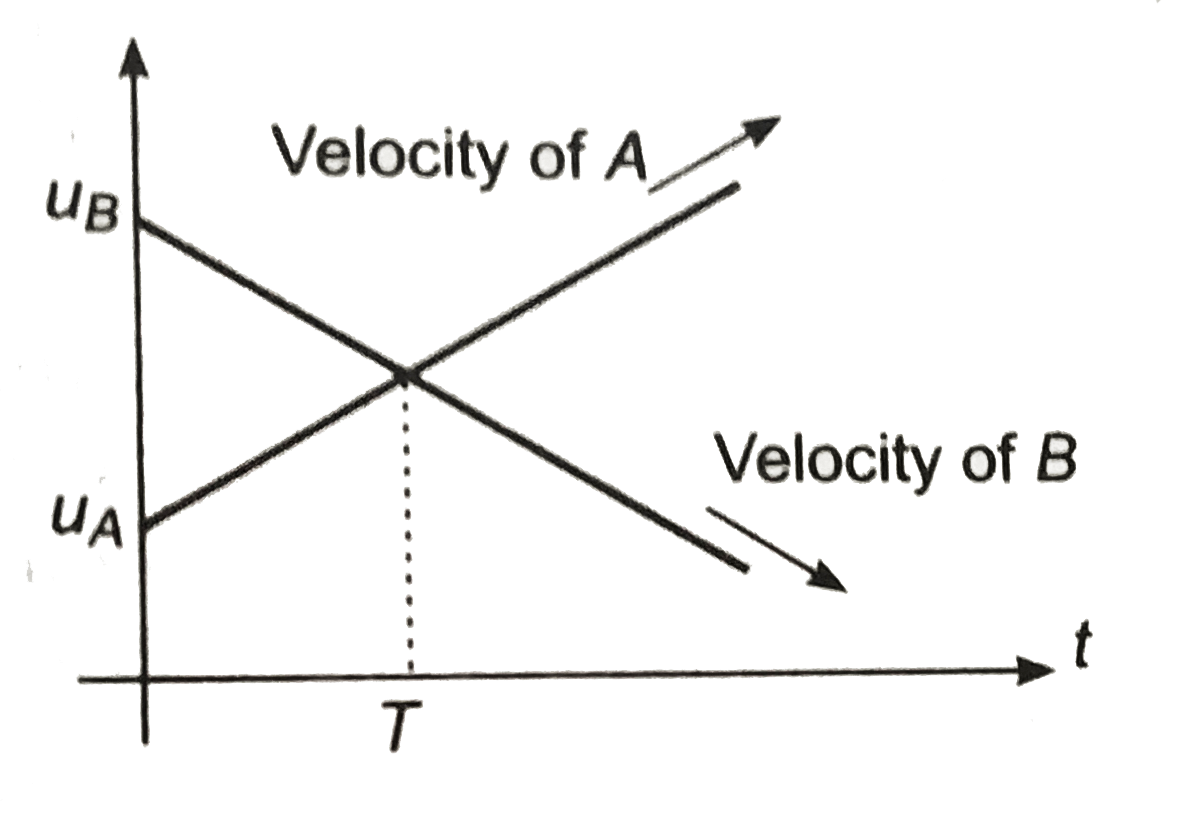
View SolutionAn object is placed in front of two convex lenses one by one at a distance u from the lens. The focal lengths of the lenses are 30 cm and 15 cm respectively. If the size of image formed in the two cases is same, then u is
View SolutionA stone is dropped from a balloon ascending with v0=2ms, from a height h=4.8 m .Find the time of flight of the stone.
View Solution
