A particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
To solve the problem, we need to calculate the total distance S traveled by the particle during the time intervals given, and then find the ratio Sa0t20.
1. Calculate the distance traveled in the first time interval t0:
- The particle starts from rest, so the initial velocity u=0.
- The acceleration during this interval is a0.
- Using the formula for distance:
S1=ut+12at2=0⋅t0+12a0t20=12a0t20
2. Calculate the final velocity at the end of the first interval:
- Using the formula v=u+at:
v=0+a0t0=a0t0
3. Calculate the distance traveled in the second time interval 2t0:
- The initial velocity for this interval is v=a0t0.
- The acceleration during this interval is 2a0.
- Using the distance formula again:
S2=ut+12at2=(a0t0)(2t0)+12(2a0)(2t0)2
- Simplifying this:
S2=2a0t20+12(2a0)(4t20)=2a0t20+4a0t20=6a0t20
4. Calculate the total distance S:
- The total distance traveled by the particle in the time 3t0 is:
S=S1+S2=12a0t20+6a0t20=12a0t20+122a0t20=132a0t20
5. Calculate Sa0t20:
- Now we compute the ratio:
Sa0t20=132a0t20a0t20=132=6.5
Final Answer:
Sa0t20=6.5
- The particle starts from rest, so the initial velocity u=0.
- The acceleration during this interval is a0.
- Using the formula for distance:
S1=ut+12at2=0⋅t0+12a0t20=12a0t20
- Using the formula v=u+at:
v=0+a0t0=a0t0
- The initial velocity for this interval is v=a0t0.
- The acceleration during this interval is 2a0.
- Using the distance formula again:
S2=ut+12at2=(a0t0)(2t0)+12(2a0)(2t0)2
- Simplifying this:
S2=2a0t20+12(2a0)(4t20)=2a0t20+4a0t20=6a0t20
- The total distance traveled by the particle in the time 3t0 is:
S=S1+S2=12a0t20+6a0t20=12a0t20+122a0t20=132a0t20
- Now we compute the ratio:
Sa0t20=132a0t20a0t20=132=6.5
Sa0t20=6.5
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)19videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)14videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 175videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)1videos
JEE MAIN REVISON TEST-23
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
Similar Questions
A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
 View Solution
View SolutionA particle starts from rest at time t=0 and moves on a straight line with acceleration as plotted in fig. The speed of the particle will be maximum after time.
 View Solution
View SolutionA body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
View SolutionA particle starting from rest moves with constant acceleration. If it takes 5.0 s to reash the speed 18.0 km/h find a. the average velocity during this period, and b. the distance travelled by the particle during this period.
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
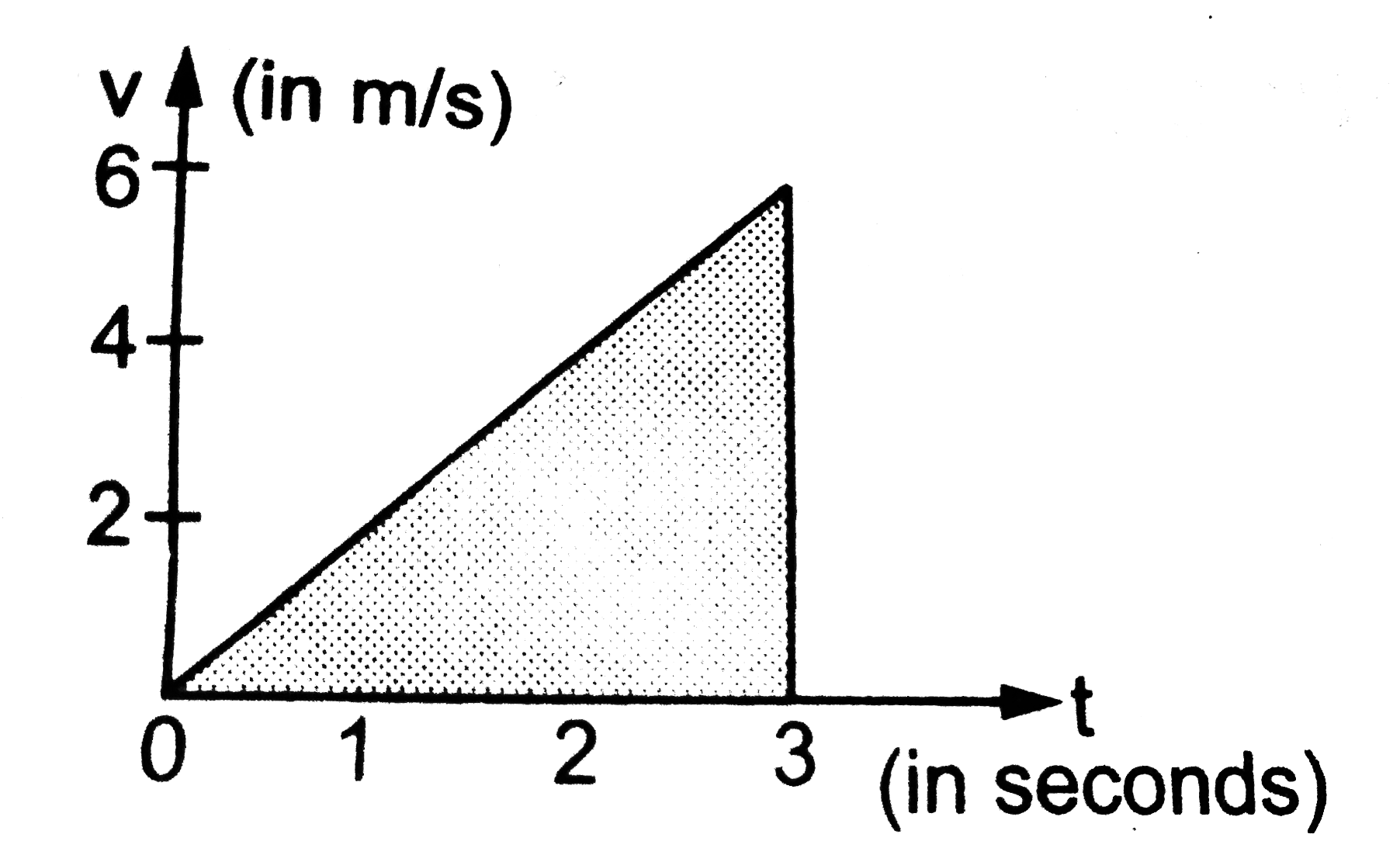 View Solution
View SolutionA car, starting from rest, accelerates at the rate f through a distance s, then continues at constant speed for time t and then decelerates at the rate f/ 2 to come to rest. If the total distance travelled is 15 s, then
View SolutionA car, starating from rest, accelerates at the rate f through a distance S, then continoues at constant speed for time t and then decelerates as the rate f/2 to come to rest. If the total distance travelled is 15 S, then
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionA particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of displacement (a) in successive second and (b) in successive time interval t0.
View Solution

