body moves along x-axis with velocity v = 5 sin(2t)m/s starting from xi=−2.5mRatio of displacement to distance traveled by body from t=0stot=3π/2sec is :
1:1
0
1:3
1:2
The correct Answer is:C
To solve the problem step by step, we will follow these instructions:
Step 1: Write the velocity function
The velocity of the body is given as:
v(t)=5sin(2t)m/s
Step 2: Relate velocity to displacement
We know that velocity is the derivative of displacement with respect to time:
v=dxdt
This implies:
dx=vdt
Substituting the velocity function:
dx=5sin(2t)dt
Step 3: Integrate to find displacement
To find the displacement x, we integrate the equation from t=0 to t=T:
x=∫T05sin(2t)dt
Calculating the integral:
x=5(−12cos(2t))T0
x=−52(cos(2T)−cos(0))
x=−52(cos(2T)−1)
Step 4: Substitute limits for T=3π2
Now, we substitute T=3π2:
x=−52(cos(3π)−1)
Since cos(3π)=−1:
x=−52(−1−1)
x=−52(−2)
x=5m
Step 5: Calculate the total distance traveled
The body moves from xi=−2.5m to xf=5m. The total distance traveled is the sum of the distances in each segment of the motion:
1. From −2.5 to 5 (forward): 5−(−2.5)=7.5m
2. The body also returns back to −2.5 before reaching 5 again, which adds another 7.5m.
Thus, the total distance traveled is:
Total Distance=7.5+7.5=15m
Step 6: Calculate the ratio of displacement to distance
The displacement is 5m and the total distance traveled is 15m. Therefore, the ratio of displacement to distance is:
Ratio=DisplacementDistance=515=13
Final Answer
The ratio of displacement to distance traveled by the body from t=0 to t=3π2 seconds is:
13
---
The velocity of the body is given as:
v(t)=5sin(2t)m/s
We know that velocity is the derivative of displacement with respect to time:
v=dxdt
This implies:
dx=vdt
Substituting the velocity function:
dx=5sin(2t)dt
To find the displacement x, we integrate the equation from t=0 to t=T:
x=∫T05sin(2t)dt
Calculating the integral:
x=5(−12cos(2t))T0
x=−52(cos(2T)−cos(0))
x=−52(cos(2T)−1)
Now, we substitute T=3π2:
x=−52(cos(3π)−1)
Since cos(3π)=−1:
x=−52(−1−1)
x=−52(−2)
x=5m
The body moves from xi=−2.5m to xf=5m. The total distance traveled is the sum of the distances in each segment of the motion:
1. From −2.5 to 5 (forward): 5−(−2.5)=7.5m
2. The body also returns back to −2.5 before reaching 5 again, which adds another 7.5m.
Total Distance=7.5+7.5=15m
The displacement is 5m and the total distance traveled is 15m. Therefore, the ratio of displacement to distance is:
Ratio=DisplacementDistance=515=13
The ratio of displacement to distance traveled by the body from t=0 to t=3π2 seconds is:
13
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)
19 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 1
75 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
body moves along x-axis with velocity v = 5 sin(2t)m/s starting from xi=−2.5m
Which of the following statements are correct ?
View SolutionFind the distance travelled by a body having velocity v=1−t2 from t = 0 to t = 2 sec .
View SolutionAssertion : A body is moving along a straight line such the its velocity varies with a time as shown in figure. Magnmitude of displacement of the body from t = 0 to t = 12 s is the same as the distance travelled by it in the given time duration.

Reason : For unidirectional motion of a body,
|displacement|=distance
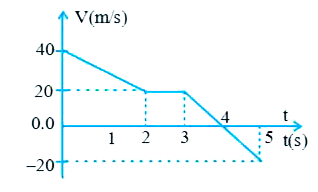
View SolutionIn the given v-t graph, the distance travelled by the body in 5 sec will be :
View SolutionA body starting from rest has an acceleration of 5m/s2. Calculate the distance travelled by it in 4th second.
View SolutionA particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Distance travelled by particle in 0 to 3 second time interval is :
View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View SolutionA particle moves along the x - axis according to x=A[1+sinωt]. What distance does is travel in time interval from t=0 to t=2.5π/ω ?
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View Solution
