A golf ball of mass m is hit by a golf club so that the ball leaves the tee with speed v. The club is in contact with the ball for time T. The magnitude of the average force on the club on the ball during the time T is :
mvT
mv/T
(1/2)mv2T
mv2(2T)
The correct Answer is:B
To find the magnitude of the average force exerted by the golf club on the golf ball during the time T, we can use the impulse-momentum theorem. The average force can be calculated using the change in momentum of the ball over the time interval T.
1. Identify the given values:
- Mass of the golf ball: m
- Final velocity of the ball after being hit: v
- Initial velocity of the ball before being hit: u=0 (the ball is at rest)
- Time of contact between the club and the ball: T
2. Calculate the change in momentum (Δp):
- The momentum before the impact:
pi=m⋅u=m⋅0=0
- The momentum after the impact:
pf=m⋅v
- Therefore, the change in momentum is:
Δp=pf−pi=m⋅v−0=m⋅v
3. Use the impulse-momentum theorem:
- The average force (Favg) can be calculated using the formula:
Favg=ΔpΔt
- Substituting the values we found:
Favg=m⋅vT
4. Final expression for the average force:
- Thus, the magnitude of the average force exerted by the club on the ball during the time T is:
Favg=m⋅vT
Final Answer:
Favg=m⋅vT
- Mass of the golf ball: m
- Final velocity of the ball after being hit: v
- Initial velocity of the ball before being hit: u=0 (the ball is at rest)
- Time of contact between the club and the ball: T
- The momentum before the impact:
pi=m⋅u=m⋅0=0
- The momentum after the impact:
pf=m⋅v
- Therefore, the change in momentum is:
Δp=pf−pi=m⋅v−0=m⋅v
- The average force (Favg) can be calculated using the formula:
Favg=ΔpΔt
- Substituting the values we found:
Favg=m⋅vT
- Thus, the magnitude of the average force exerted by the club on the ball during the time T is:
Favg=m⋅vT
Favg=m⋅vT
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - Level - 1 PARAGRAPH QUESTIONS3videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 248videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 0 - LONG ANSWER TYPE5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
A golf player hits a golf ball of mass 100 g and imparts it a speed of 50 m/s. If golf stick remains in contact with the ball for 0.01 s, then the average force exerted by the golf stick on the ball.
View SolutionA 150 g tenins ball coming at a speed of 40m/s is hit straight back by a bat to speed of 60m/s. The magnitude of the average force F on the ball, when it is in contact for 5ms is,
View Solution
Knowledge Check
- Question 1 - Select One
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzero - Question 2 - Select One
A ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2mu - Question 3 - Select One
A ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
A ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
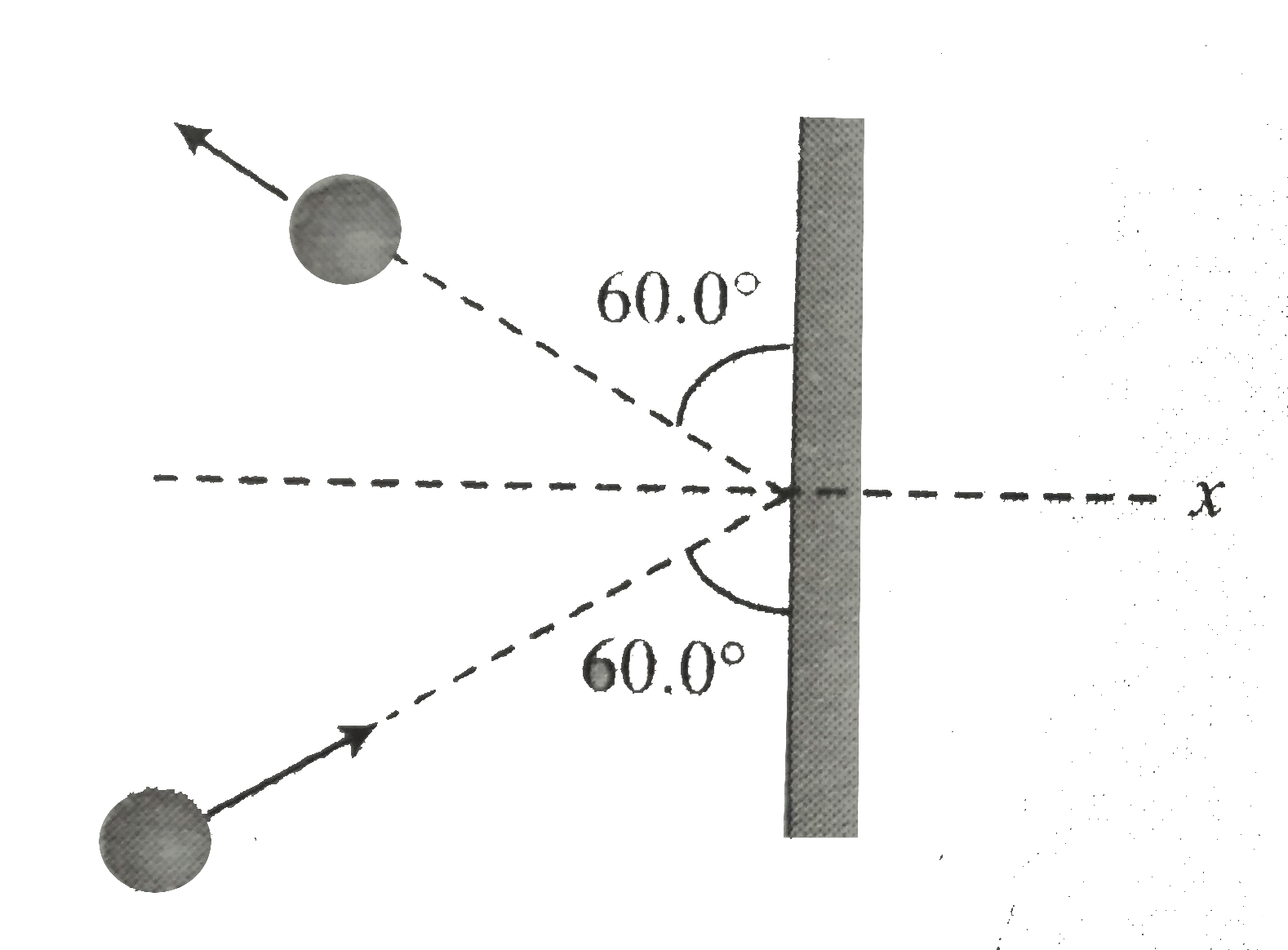 View Solution
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
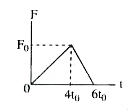
Average force exerted by the bat on the ball isView Solution

