An engine pumps water continously through a hole. The speed with which water pases through the hole nozzle is v and k is the mass per unit length of the water jet as it leaves the nozzle. Find the rate at which kinetic energy is being imparted to the water.
12kv2
12kv3
v22k
v32k
The correct Answer is:B
To find the rate at which kinetic energy is being imparted to the water, we can follow these steps:
Step 1: Understand the relationship between mass and length
We are given that k is the mass per unit length of the water jet. This can be expressed mathematically as:
k=dmdx
where dm is the mass of the water and dx is the length of the water jet.
Step 2: Define the kinetic energy
The kinetic energy (KE) of a mass m moving with a velocity v is given by the formula:
KE=12mv2
Step 3: Express the rate of change of kinetic energy
To find the rate at which kinetic energy is being imparted to the water, we need to calculate the time derivative of kinetic energy:
d(KE)dt=ddt(12mv2)
Step 4: Apply the chain rule
Using the chain rule, we can express this as:
d(KE)dt=12⋅v2⋅dmdt
Step 5: Relate mass flow rate to velocity
The mass flow rate (dmdt) can be expressed in terms of the mass per unit length and the velocity of the water:
dmdt=dmdx⋅dxdt=k⋅v
Here, dxdt=v is the velocity of the water jet.
Step 6: Substitute back into the kinetic energy equation
Now substituting dmdt back into the kinetic energy rate equation:
d(KE)dt=12v2⋅(k⋅v)
This simplifies to:
d(KE)dt=12kv3
Final Result
Thus, the rate at which kinetic energy is being imparted to the water is:
d(KE)dt=12kv3
---
We are given that k is the mass per unit length of the water jet. This can be expressed mathematically as:
k=dmdx
where dm is the mass of the water and dx is the length of the water jet.
The kinetic energy (KE) of a mass m moving with a velocity v is given by the formula:
KE=12mv2
To find the rate at which kinetic energy is being imparted to the water, we need to calculate the time derivative of kinetic energy:
d(KE)dt=ddt(12mv2)
Using the chain rule, we can express this as:
d(KE)dt=12⋅v2⋅dmdt
The mass flow rate (dmdt) can be expressed in terms of the mass per unit length and the velocity of the water:
dmdt=dmdx⋅dxdt=k⋅v
Here, dxdt=v is the velocity of the water jet.
Now substituting dmdt back into the kinetic energy rate equation:
d(KE)dt=12v2⋅(k⋅v)
This simplifies to:
d(KE)dt=12kv3
Thus, the rate at which kinetic energy is being imparted to the water is:
d(KE)dt=12kv3
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
An engine pumps water continously through a hose. Water leave the hose with a velocity v and m is the mass per unit length of the Water jet. What is the rate at Which kinetic energy is imparted to water?
View SolutionAn engine pumps water continously through a hose. Water leave the hose with a velocity v and m is the mass per unit length of the Water jet. What is the rate at Which kinetic energy is imparted to water?
View SolutionAn engine pumps liquid of density ρ continuously through a pipe of cross-section area A. If the speed with which liquid passes through the pipe is v, then the rate at which kinetic energy is being imparted to the liquid by the pump is
View SolutionThe part of plant through which water reaches up to the leaves.
View SolutionAn engine pumps water through a hose pipe. Water passes through the pipe and leaves it with a velocity of 2ms1. The mass per unit length of water in the pipe is 100kgm−1. What is the power of the engine?
(a) 400 W (b) 200W (c) 100W (d) 800W
View SolutionA pump ejects 12000 kg of water at speed of 4m/s in 40 second. Find the average rate at which the pump is working.
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.
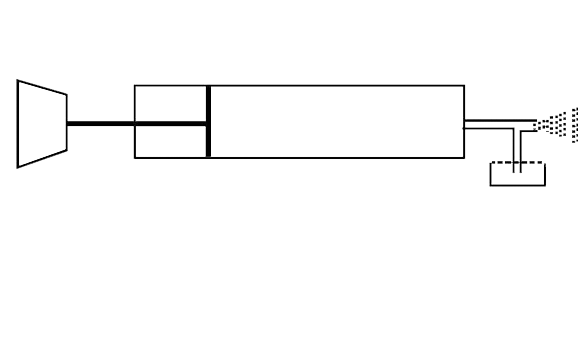
If the density of air is ρa, and that of the liquid ρl, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to
View SolutionWater flows through a hose (pipe) whose internal diameter is 2 cm at a speed of 1 m/s. What should be the diameter of the nozzle if the water is to emerge at a speed of 4 m/s
View SolutionFigure shows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure 2p0 where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.

View SolutionAn engine pumps 800 kg of water through height of 10 m in 80 s. Find the power of the engine if its efficiency is 75%
View Solution