A spring of force constant 800 N/m has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is:
16 J
8 J
32 J
24 J
The correct Answer is:B
To solve the problem of finding the work done in extending a spring from 5 cm to 15 cm, we can follow these steps:
Step 1: Understand the formula for work done on a spring
The work done (W) in extending a spring can be calculated using the formula:
W=12k(x22−x21)
where:
- k is the force constant of the spring (in N/m),
- x1 is the initial extension (in m),
- x2 is the final extension (in m).
Step 2: Convert the extensions from centimeters to meters
The extensions given are in centimeters, so we need to convert them to meters:
- x1=5cm=0.05m
- x2=15cm=0.15m
Step 3: Substitute the values into the formula
Now, we can substitute the values into the work done formula:
- k=800N/m
- x1=0.05m
- x2=0.15m
Substituting these values into the formula gives:
W=12×800×(0.152−0.052)
Step 4: Calculate the squares of the extensions
Now we calculate the squares:
- 0.152=0.0225
- 0.052=0.0025
Step 5: Substitute the squared values back into the formula
Now substitute these squared values back into the equation:
W=12×800×(0.0225−0.0025)
W=12×800×0.02
Step 6: Calculate the work done
Now we can calculate the work done:
W=12×800×0.02
W=400×0.02
W=8J
Final Answer
The work done in extending the spring from 5 cm to 15 cm is 8 Joules.
---
The work done (W) in extending a spring can be calculated using the formula:
W=12k(x22−x21)
where:
- k is the force constant of the spring (in N/m),
- x1 is the initial extension (in m),
- x2 is the final extension (in m).
The extensions given are in centimeters, so we need to convert them to meters:
- x1=5cm=0.05m
- x2=15cm=0.15m
Now, we can substitute the values into the work done formula:
- k=800N/m
- x1=0.05m
- x2=0.15m
W=12×800×(0.152−0.052)
Now we calculate the squares:
- 0.152=0.0225
- 0.052=0.0025
Now substitute these squared values back into the equation:
W=12×800×(0.0225−0.0025)
W=12×800×0.02
Now we can calculate the work done:
W=12×800×0.02
W=400×0.02
W=8J
The work done in extending the spring from 5 cm to 15 cm is 8 Joules.
Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE)
80 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
5 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS
2 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
View SolutionFind the ratio of 90 cm to 1.5 m.
View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionWhen a load of 10 kg is hung from the wire, then extension of 2m is produced. Then work done by restoring force is
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
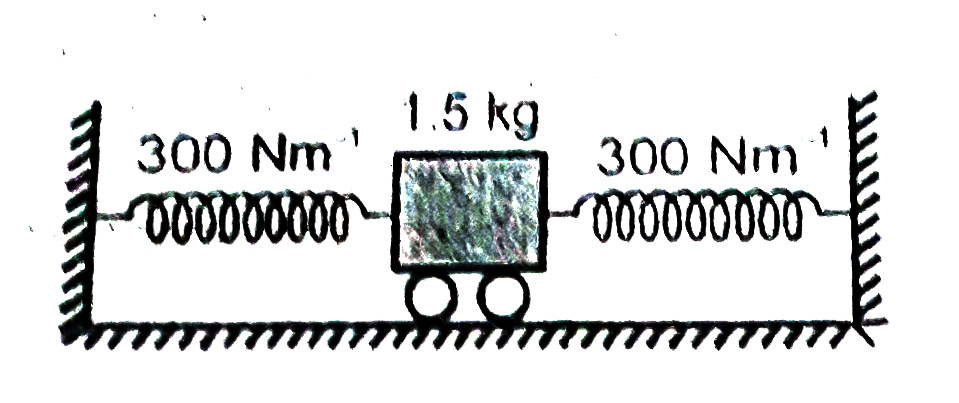
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA force F is exerted on a body of mass M, which is connected to a spring (spring constant k). The body has a constant acceleration a. Calculate the work done by the external force in moving the body by a distance D.
View Solution
