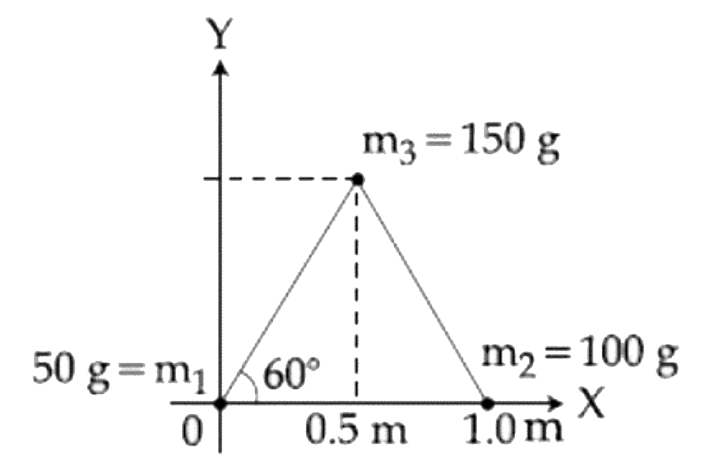
Three particles of masses 50g,100g and 150g are placed at the vertices of an equilateral triangle of side 1m (as shown in the figure). The (x,y) coordinates of the centre of mass will be :
 .
.
(712m,√34m)
(√34m,512m)
(712m,√38m)
(√38m,712m)
The correct Answer is:A
Coordinates of the masses:
m1:(0,0) m2:(1,0) m3=10.5,0.5√350+100+150=√34m
Coordinates of CM : (712,√34).
Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE)
80 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
5 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS
2 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
Three particles of massses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side 1m ( as shown in the figure ) . The ( x, y) coordinates of the centre of mass will be :
View SolutionFind the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
View Solution
Knowledge Check
Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
Three particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png)
View SolutionThree particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png)
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
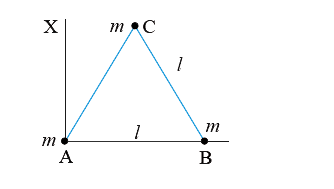
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionThree masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
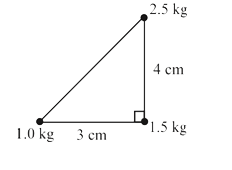
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :

View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View Solution
